
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈(0,1),给出以下命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈(0,1),给出以下命题:| A. | 0 | B. | 3 | C. | 2 | D. | 1 |
分析 根据已知中正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),逐一分析四个结论的真假,可得答案.
解答 解:对于①,∵平面ADD′A′∥平面BCC′B′,∴EN∥MF,同理:FN∥EM,∴四边形EMFN为平行四边形,故正确;
对于②,MENF的面积s=f(x)=$\frac{1}{2}$(EF×MN),当M为BB′的中点时,即x=$\frac{1}{2}$时,MN最短,此时面积最小.故正确;
对于③,连结AF,AM,AN,则四棱锥则分割为两个小三棱锥,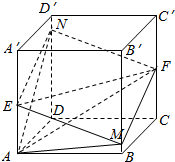
它们以AEF为底,以M,N分别为顶点的两个小棱锥.因为三角形AEF的面积是个常数.M,N到平面AEF的距离和是个常数,所以四棱锥C'-MENF的体积V为常数函数,故正确.
对于④,多面体ABCD-MENF的体积V=h(x)=$\frac{1}{2}$VABCD-A′B′C′D′=$\frac{1}{2}$为常数函数,故错误;
对于⑤,当x=$\frac{1}{2}$时,四边形MENF为正方形.正确;
故选:D
点评 本题考查空间立体几何中的面面垂直关系以及空间几何体的体积公式,本题巧妙的把立体几何问题和函数进行的有机的结合,综合性较强,设计巧妙,对学生的解题能力要求较高.属于中档题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:选择题
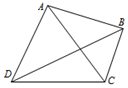 蓝军和红军进行军事演练,蓝军在距离$\sqrt{3}$的军事基地C和D,测得红军的两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,则红军这两支精锐部队间的距离是( )
蓝军和红军进行军事演练,蓝军在距离$\sqrt{3}$的军事基地C和D,测得红军的两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,则红军这两支精锐部队间的距离是( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{3}{4}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com