
【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C: ![]() =1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求 ![]() 的值;
的值;
(3)记直线l与y轴的交点为P.若 ![]() =
= ![]()
![]() ,求直线l的斜率k.
,求直线l的斜率k.
【答案】
(1)
解:因为椭圆椭圆C: ![]() =1经过点(b,2e)所以
=1经过点(b,2e)所以 ![]() .
.
因为e2= ![]() ,所以
,所以 ![]() ,
,
又∵a2=b2+c2, ![]() ,解得b2=4或b2=8(舍去).
,解得b2=4或b2=8(舍去).
所以椭圆C的方程为 ![]()
(2)
解:设A(x1,y1),B(x2,y2).
因为T(1,0),则直线l的方程为y=k(x﹣1).
联立直线l与椭圆方程 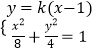 ,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,
,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,
所以x1+x2= ![]() ,x1x2=
,x1x2= ![]() .
.
因为MN∥l,所以直线MN方程为y=kx,
联立直线MN与椭圆方程 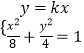
消去y得(2k2+1)x2=8,
解得x2= ![]()
因为MN∥l,所以 ![]()
因为(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]= ![]() .
.
(xM﹣xN)2=4x2= ![]() .
.
所以 ![]() =
= ![]()
(3)
解:在y=k(x﹣1)中,令x=0,则y=﹣k,所以P(0,﹣k),
从而 ![]() ,
,
∵ ![]() =
= ![]()
![]() ,
, ![]() …①
…①
由(2)知 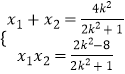 …②
…②
由①②得 ![]() 50k4﹣83k2﹣34=0,解得k2=2或k2=﹣
50k4﹣83k2﹣34=0,解得k2=2或k2=﹣ ![]() (舍).
(舍).
又因为k>0,所以k= ![]()
【解析】(1)由题意得e2= ![]() ,
, ![]() .又a2=b2+c2 ,
.又a2=b2+c2 , ![]() ,解得b2;(2)设A(x1 , y1),B(x2 , y2).设直线l的方程为y=k(x﹣1).
,解得b2;(2)设A(x1 , y1),B(x2 , y2).设直线l的方程为y=k(x﹣1).
联立直线l与椭圆方程 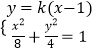 ,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,可设直线MN方程为y=kx,联立直线MN与椭圆方程
,消去y,得(2k2+1)x2﹣4k2x+2k2﹣8=0,可设直线MN方程为y=kx,联立直线MN与椭圆方程 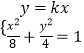 ,消去y得(2k2+1)x2=8,由MN∥l,得
,消去y得(2k2+1)x2=8,由MN∥l,得 ![]()
由(1﹣x1)(x2﹣1)=﹣[x1x2﹣(x1+x2)+1]= ![]() .得(xM﹣xN)2=4x2=
.得(xM﹣xN)2=4x2= ![]() .即可. (3)在y=k(x﹣1)中,令x=0,则y=﹣k,所以P(0,﹣k),从而
.即可. (3)在y=k(x﹣1)中,令x=0,则y=﹣k,所以P(0,﹣k),从而 ![]() ,由
,由 ![]() =
= ![]()
![]() 得
得 ![]() …①,由(2)知
…①,由(2)知 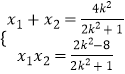 …②由①②得
…②由①②得 ![]() 50k4﹣83k2﹣34=0,解得k2
50k4﹣83k2﹣34=0,解得k2
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


科目:高中数学 来源: 题型:
【题目】选修4﹣﹣4;坐标系与参数方程
已知动点P,Q都在曲线C: ![]() 上,对应参数分别为β=α与β=2α(0<α<2π),M为PQ的中点.
上,对应参数分别为β=α与β=2α(0<α<2π),M为PQ的中点.
(1)求M的轨迹的参数方程
(2)将M到坐标原点的距离d表示为α的函数,并判断M的轨迹是否过坐标原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自“钓鱼岛事件”以来,中日关系日趋紧张并不断升级.为了积极响应“保钓行动”,某学校举办了一场“保钓知识大赛”,共分两组.其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的同学中,每组各任选1个同学,作为“保钓行动代言人”.
(1)求选出的2个同学中恰有1个女生的概率;
(2)设X为选出的2个同学中女生的个数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价x和销售量y之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量(件) | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列3项抽样调查:
①从15种疫苗中抽取5种检测是否合格.
②涡阳县某中学共有480名教职工,其中一线教师360名,行政人员48名,后勤人员72名.为了解教职工对学校校务公开方面的意见,拟抽取一个容量为20的样本.
③涡阳县某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.
较为合理的抽样方法是( )
A. ①简单随机抽样, ②系统抽样, ③分层抽样
B. ①简单随机抽样, ②分层抽样, ③系统抽样
C. ①系统抽样, ②简单随机抽样, ③分层抽样
D. ①分层抽样, ②系统抽样, ③简单随机抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若存在实数
,若存在实数![]() ,使得对于任意的
,使得对于任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“
为“![]() 数列”( )
数列”( )
A. 若![]() 是等差数列,且首项
是等差数列,且首项![]() ,则数列
,则数列![]() 是“
是“![]() 数列”
数列”
B. 若![]() 是等差数列,且公差
是等差数列,且公差![]() ,则数列
,则数列![]() 是“
是“![]() 数列”
数列”
C. 若![]() 是等比数列,也是“
是等比数列,也是“![]() 数列”,则数列
数列”,则数列![]() 的公比
的公比![]() 满足
满足![]()
D. 若![]() 是等比数列,且公比
是等比数列,且公比![]() 满足
满足![]() ,则数列
,则数列![]() 是“
是“![]() 数列”
数列”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 数列{bn},{cn}满足 (n+1)bn=an+1﹣ ![]() ,(n+2)cn=
,(n+2)cn= ![]() ﹣
﹣ ![]() ,其中n∈N*.
,其中n∈N*.
(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切n∈N*,有bn≤λ≤cn , 求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某舆情机构为了解人们对某事件的关注度,随机抽取了![]() 人进行调查,其中女性中对该事件关注的占
人进行调查,其中女性中对该事件关注的占![]() ,而男性有
,而男性有![]() 人表示对该事件没有关注.
人表示对该事件没有关注.
关注 | 没关注 | 合计 | |
男 |
| ||
女 | |||
合计 |
(1)根据以上数据补全![]() 列联表;
列联表;
(2)能否有![]() 的把握认为“对事件是否关注与性别有关”?
的把握认为“对事件是否关注与性别有关”?
(3)已知在被调查的女性中有![]() 名大学生,这其中有
名大学生,这其中有![]() 名对此事关注.现在从这
名对此事关注.现在从这![]() 名女大学生中随机抽取
名女大学生中随机抽取![]() 人,求至少有
人,求至少有![]() 人对此事关注的概率.
人对此事关注的概率.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com