
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用类比推理可得出相应的结论,但是得出的结论不一定正确.
解答 解:①由实数的乘法法则满足交换率“mn=nm”类比得到向量也满足交换率“$\overrightarrow a•\overrightarrow b=\overrightarrow b•\overrightarrow a$”,正确;
②由实数的乘法法则满足分配律“(m+n)t=mt+nt”类比得到向量也满足分配律“$(\overrightarrow a+\overrightarrow b)•\overrightarrow c=\overrightarrow a•\overrightarrow c+\overrightarrow b•\overrightarrow c$”,正确;
③由实数的乘法法则满足结合律“(m•n)t=m(n•t)”类比得到“$(\overrightarrow a•\overrightarrow b)•\overrightarrow c=\overrightarrow a•(\overrightarrow b•\overrightarrow c)$”,不正确,因为向量$\overrightarrow{c}$与$\overrightarrow{a}$不一定共线;
④由实数的乘法满足消去率“t≠0,mt=xt⇒m=x”类比得到向量满足“$\overrightarrow c≠\overrightarrow 0,\overrightarrow a•\overrightarrow c=\overrightarrow b•\overrightarrow c⇒\overrightarrow a=\overrightarrow b$”,不正确,∵若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$$⊥\overrightarrow{c}$,$\overrightarrow{b}$⊥$\overrightarrow{c}$,则$\overrightarrow{a}•\overrightarrow{c}=\overrightarrow{b}•\overrightarrow{c}$,但是$\overrightarrow{a}$=$\overrightarrow{b}$不一定成立;
综上可知:类比得到的结论正确的是①②,个数是2.
故选B.
点评 正确理解类比推理的意义和内容是解题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
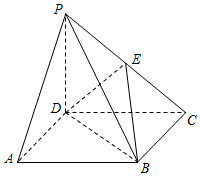 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD垂直于底面ABCD,PD=DC,点E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
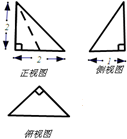
| A. | $\frac{2}{3}$ | B. | $3+\sqrt{2}+\sqrt{3}$ | C. | 2 | D. | $1+2\sqrt{2}+\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 7 | 14 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 17 | x | 4 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 4 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com