
分析 (1)由直线l:x+y=b与抛物线C:y2=2px联立,消去x整理成关于y的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,$\overrightarrow{OA}•\overrightarrow{OB}$=x1•x2+y1•y2=8,由韦达定理得方程,结合C的焦点F到直线1的距离为$\frac{7\sqrt{2}}{4}$,求出b,p,即可求抛物线C的方程;
(2)求出A,B的坐标,利用待定系数法求△OAB外接圆的方程.
解答 解:(1)由直线l:x+y=b与抛物线C:y2=2px,得y2+2py-2pb=0,
设A(x1,y1),B(x2,y2),
则y1•y2=-2pb,y1+y2=-2p
x1•x2=(b-y1)•(b-y2)=b2,
∵$\overrightarrow{OA}•\overrightarrow{OB}$=8,∴x1•x2+y1•y2=b2-2pb=8,
∵C的焦点F到直线1的距离为$\frac{7\sqrt{2}}{4}$,
∴$\frac{|\frac{p}{2}-b|}{\sqrt{2}}$=$\frac{7\sqrt{2}}{4}$,
∵b>p>0,∴b=4,p=1,
∴抛物线C的方程y2=2x;
(2)由(1)y2+2y-8=0,∴y=2或-4,
∴A(2,2),B(8,-4)
设△OAB外接圆的方程为x2+y2+Dx+Ey=0,
A,B代入可得$\left\{\begin{array}{l}{4+4+2D+2E=0}\\{64+16+8D-4E=0}\end{array}\right.$,∴D=-8,E=4,
∴△OAB外接圆的方程为x2+y2-8x+4y=0.
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查圆的方程,考查学生分析解决问题的能力,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
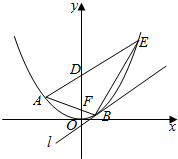 如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l
如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-1,+∞) | C. | [1,+∞) | D. | [-1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com