
分析 (1)不等式|2x-2|<|x-4|,即 (2x-2)2<(x-4)2,由此求得不等式的解集.
(2)由题意可得-2<a<2,-2<b<2,用比较法证得|4+ab|2-(2|a+b|)2>0,可得不等式 2|a+b|<|4+ab|成立.
解答 解:(1)不等式:|2x-2|<|x-4|,即 (2x-2)2<(x-4)2,即 3x2<12,
求得-2<x<2,故不等式的解集为(-2,2).
(2)记(1)中不等式的解集为A,当a,b∈A时,有-2<a<2,-2<b<2.
∵|4+ab|2-(2|a+b|)2=16+8ab+a2•b2-4(a2+2ab+b2)
=16+a2•b2-4a2-4b2=4(4-b2)+a2(b2-4)=(4-b2)(4-a2)>0,
∴|4+ab|>2|a+b|,即 不等式 2|a+b|<|4+ab|成立.
点评 本题考查绝对值函数,考查解不等式,考查不等式的证明,解题的关键是将不等式写成分段函数,利用作差法证明不等式,属于中档题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{55}}}{5}$ | B. | $\frac{22}{5}$ | C. | $\frac{{2\sqrt{11}}}{5}$ | D. | $\frac{{22\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
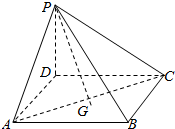 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,ABCD为正方形,且PD=AB=1,G为△ABC的重心,则PG与底面所成的角θ满足( )| A. | θ=$\frac{π}{4}$ | B. | cosθ=$\frac{2\sqrt{34}}{17}$ | C. | tanθ=$\frac{2\sqrt{2}}{3}$ | D. | sinθ=$\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com