
 b)和点N(x0,y0),则称直线l:ax0x+by0y=1为椭圆C的“伴随直线”,
b)和点N(x0,y0),则称直线l:ax0x+by0y=1为椭圆C的“伴随直线”,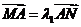 ,
,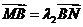 ,问
,问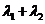 是否为定值?说明理由.
是否为定值?说明理由.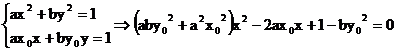
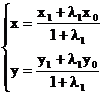 代入椭圆C:ax2+by2=1,利用M在l上,
代入椭圆C:ax2+by2=1,利用M在l上,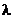 12+ax12+by12–1=0
12+ax12+by12–1=0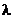 2的方程,类似.
2的方程,类似.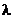 1、
1、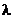 2是(ax02+by02–1)
2是(ax02+by02–1)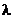 2+ax12+by12–1=0的两根
2+ax12+by12–1=0的两根

科目:高中数学 来源:不详 题型:解答题
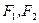 是椭圆
是椭圆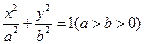 的两个焦点,
的两个焦点,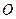 为坐标原点,点
为坐标原点,点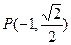 在椭圆上,且
在椭圆上,且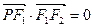 ,⊙
,⊙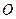 是以
是以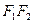 为直径的圆,直线
为直径的圆,直线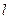 :
: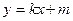 与⊙
与⊙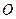 相切,并且与椭圆交于不同的两点
相切,并且与椭圆交于不同的两点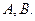
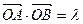 ,且满足
,且满足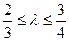 时,求弦长
时,求弦长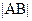 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
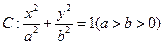 经过点
经过点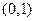 ,离心率
,离心率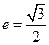 。
。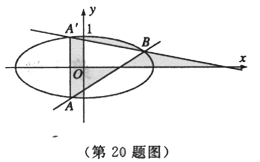
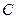 的方程;
的方程;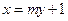 与椭圆
与椭圆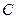 交于
交于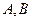 两点,点
两点,点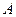 关于
关于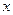 轴的对称点为
轴的对称点为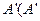 与
与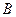 不重合),则直线
不重合),则直线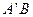 与
与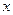 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 :
: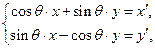 可把平面直角坐标系上的点
可把平面直角坐标系上的点 变换到这一平面上的点
变换到这一平面上的点 .特别地,若曲线
.特别地,若曲线 上一点
上一点 经变换公式
经变换公式 变换后得到的点
变换后得到的点 与点
与点 重合,则称点
重合,则称点 是曲线
是曲线 在变换
在变换 下的不动点.
下的不动点. 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 的标准方程. 并求出当
的标准方程. 并求出当 时,其两个焦点
时,其两个焦点 、
、 经变换公式
经变换公式 变换后得到的点
变换后得到的点 和
和 的坐标;
的坐标; 时,求(1)中的椭圆
时,求(1)中的椭圆 在变换
在变换 下的所有不动点的坐标;
下的所有不动点的坐标; :
: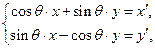 (
( ,
,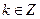 )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
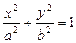 (
(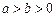 )的离心率为
)的离心率为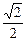 ,且短轴长为2.
,且短轴长为2.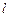 与椭圆交于
与椭圆交于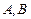 两点,
两点,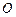 为坐标原点,且
为坐标原点,且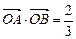 ,
,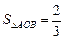 ,求直线
,求直线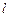 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
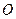 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为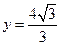 ,离心率
,离心率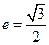 ,
,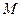 是椭圆上的动点。
是椭圆上的动点。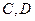 的坐标分别是
的坐标分别是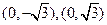 ,求
,求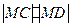 的最大值;
的最大值;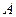 的坐标为
的坐标为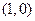 ,
,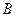 是圆
是圆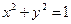 上的点,
上的点,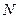 是点
是点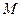 在
在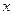 轴上的射影,点
轴上的射影,点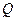 满足条件:
满足条件: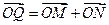 ,
,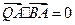 ,求线段
,求线段 的中点
的中点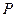 的轨迹方程。
的轨迹方程。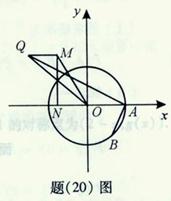
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的左、右准线分别为l1、l2,且分别交x轴于C、D两点,从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与l2交于点B,若
的左、右准线分别为l1、l2,且分别交x轴于C、D两点,从l1上一点A发出一条光线经过椭圆的左焦点F被x轴反射后与l2交于点B,若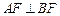 ,且
,且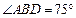 ,则椭圆的离心率等于_____________.
,则椭圆的离心率等于_____________.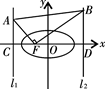
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com