
分析 (1)由等差数列的性质可知d=$\frac{{a}_{17}-{a}_{1}}{17-1}$=4,利用等差通项公式即可求得数列{an}的通项公式;
(2)当n=2012时,代入(1)所求得通项公式,即可求得a2012;
(3)令2012=4n-2,解得:n=503.5∉N +,故2012不是数列{an}中的项.
解答 解:(1)由a1=2,a17=66,
d=$\frac{{a}_{17}-{a}_{1}}{17-1}$=4,
由等差数列通项公式可知:an=4(n-1)+2=4n-2.
(2)a2012=4×2 012-2=8 046.
(3)设2012=4n-2,解得:n=503.5∉N +,
∴2012不是数列{an}中的项.
点评 本题考查等差数列的通项公式的求法,考查等差数列的性质,考查计算能力,属于基础题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | y+1=0或x=0 | B. | x+1=0或y=0 | C. | y-1=0或x=0 | D. | x-1=0或y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 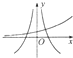 | B. | 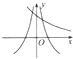 | C. | 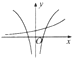 | D. | 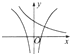 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com