
分析 方法一:第1次摸出红球,由于不放回,所以袋中还有5个不同的红球和4个不同的白球,由此可求概率,
方法二:事件“第一次摸到红球且第二次也摸到红球”的概率等于事件“第一次摸到红球”的概率乘以事件“在第一次摸出红球的条件下,第二次也摸到红球”的概率.根据这个原理,可以分别求出“第一次摸到红球”的概率和“第一次摸到红球且第二次也摸到红球”的概率,再用公式可以求出要求的概率
解答 解:方法一:由题意,第1次摸出红球,由于不放回,所以袋中还有5个不同的红球和4个不同的白球
故在第1次摸出红球的条件下,第2次摸出的也是红球的概率为$\frac{5}{4+5}$=$\frac{5}{9}$,
方法二:先求出“第一次摸到红球”的概率为:P1=$\frac{6}{10}$,
设“在第一次摸出红球的条件下,第二次也摸到红球”的概率是P2
再求“第一次摸到红球且第二次也摸到红球”的概率为P=$\frac{6×5}{10×9}$=$\frac{1}{3}$,
根据条件概率公式,得:P2=$\frac{P}{{P}_{1}}$=$\frac{5}{9}$,
故答案为:$\frac{5}{9}$
点评 本题考查了概率的计算方法,主要是考查了条件概率与独立事件的理解,属于中档题.看准确事件之间的联系,正确运用公式,是解决本题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
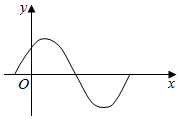
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{2}$ | C. | $-\frac{π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com