
分析 (1)利用f(1)=-f(-1),可得结论;
(2)任取x∈(0,+∞),则x∈(-∞,0),结合条件求函数f(x)在(0,+∞)上的解析式;
(3)设任取x1,x2∈(0,+∞),且x1<x2,然后作差,通分,证明f(x1)<f(x2),便可得出f(x)在(0,+∞)上单调递增
解答 解:(1)因为函数f(x)是奇函数,所以f(1)=-f(-1)=$\frac{1}{2}$.…(3分)
(2)任取x∈(0,+∞),则x∈(-∞,0),所以f(-x)=$\frac{-x}{1+x}$.…(5分)
因为f(x)是奇函数,所以f(-x)=-f(x).
所以f(x)=-f(-x)=$\frac{x}{1+x}$.…(7分)
(3)函数f(x)在(0,+∞)上为增函数.…(8分)
证明:任取x1,x2∈(0,+∞),且x1<x2.
则f(x1)-f(x2)=$\frac{{x}_{1}}{1+{x}_{1}}$-$\frac{{x}_{2}}{1+{x}_{2}}$=$\frac{{x}_{1}-{x}_{2}}{(1+{x}_{1})(1+{x}_{2})}$.…(10分)
因为x1,x2∈(0,+∞),所以1+x1,1+x2>0,
因为x1<x2,所以x1-x2<0.
因此$\frac{{x}_{1}-{x}_{2}}{(1+{x}_{1})(1+{x}_{2})}$<0,即f(x1)-f(x2)<0.
所以f(x1)<f(x2),所以函数f(x)在(0,+∞)上为增函数.…(12分)
点评 考查函数解析式及奇函数的定义,根据增函数的定义判断并证明一个函数为增函数的方法和过程,作差的方法比较f(x1),f(x2),作差后是分式的一般要通分.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
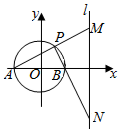 已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.
已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果两个复数的积是实数,那么这两个复数互为共轭复数 | |
| B. | 用反证法证明命题“设a,b为实数,则方程x2+ax+b=0至少有一个实根”时,要做的假设是:方程x2+ax+b=0至多有一个实根 | |
| C. | 观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…则可得到a10+b10=122 | |
| D. | 在复平面中复数z满足|z|=2的点的轨迹是以原点为圆心,以2为半径的圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
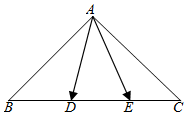 如图,在等腰直角三角形ABC中,AB=AC=$\sqrt{2}$,D,E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是( )
如图,在等腰直角三角形ABC中,AB=AC=$\sqrt{2}$,D,E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是( )| A. | $[{\frac{8}{9},\;\frac{4}{3}}]$ | B. | $[{\frac{4}{3},\;\frac{8}{3}}]$ | C. | $[{\frac{8}{9},\;\frac{8}{3}}]$ | D. | $[{\frac{4}{3},\;+∞})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com