
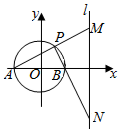
 已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.
已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.分析 (1)⊙O的方程为x2+y2=4,直线l的方程为x=6,点P的坐标为(1,$\sqrt{3}$),由此能求出以MN为直径的圆的方程.
(2)设点P的坐标为(x0,y0),则${{y}_{0}}^{2}=4-{{x}_{0}}^{2}$,求出MN的中点坐标和以MN为直径的圆C截x轴的线段长度,由此能证明以MN为直径的圆必过圆O内的一定点.
解答  解:(1)∵圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.
解:(1)∵圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.
如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy,
∴⊙O的方程为x2+y2=4,直线l的方程为x=6,
∵∠PAB=30°,∴点P的坐标为(1,$\sqrt{3}$),
∴${l}_{AP}:y=\frac{\sqrt{3}}{3}(x+2)$,${l}_{BP}:y=\sqrt{3}(x-2)$,
将x=6代入,得M(6,$\frac{8\sqrt{3}}{3}$),N(6,-4$\sqrt{3}$),
∴MN的中点坐标为(6,-$\frac{2\sqrt{3}}{3}$),MN=$\frac{20\sqrt{3}}{3}$,
∴以MN为直径的圆的方程为(x-6)2+(y+$\frac{2\sqrt{3}}{3}$)2=$\frac{100}{3}$.
同理,当点P在x轴下方时,所求圆的方程仍是(x-6)2+(y+$\frac{2\sqrt{3}}{3}$)2=$\frac{100}{3}$,
∴所求圆的方程为(x-6)2+(y+$\frac{2\sqrt{3}}{3}$)2=$\frac{100}{3}$.
证明:(2)设点P的坐标为(x0,y0),则${{x}_{0}}^{2}+{{y}_{0}}^{2}=4$,(y0≠0)
∴${{y}_{0}}^{2}=4-{{x}_{0}}^{2}$,
∵${l}_{PA}:y=\frac{{y}_{0}}{{x}_{0}+2}$,${l}_{PB}:y=\frac{{y}_{0}}{{x}_{0}-2}(x-2)$,
将x=6代入,得${y}_{M}=\frac{8{y}_{0}}{{x}_{0}+2}$,${y}_{N}=\frac{4{y}_{0}}{{x}_{0}-2}$,
∴M(6,$\frac{8{y}_{0}}{{x}_{0}+2}$),N(6,$\frac{4{y}_{0}}{{x}_{0}-2}$),MN=|$\frac{8{y}_{0}}{{x}_{0}+2}-\frac{4{y}_{0}}{{x}_{0}-2}$|=$\frac{4|{x}_{0}-6|}{|{y}_{0}|}$,
MN的中点坐标为(6,-$\frac{2(3{x}_{0}-2)}{{y}_{0}}$),
以MN为直径的圆C截x轴的线段长度为:
2$\sqrt{\frac{4({x}_{0}-6)^{2}}{{{y}_{0}}^{2}}-\frac{4(3{x}_{0}-2)}{{{y}_{0}}^{2}}}$=$\frac{4}{|{y}_{0}|}$$\sqrt{8(4-{{x}_{0}}^{2})}$=$\frac{8\sqrt{2}}{|{y}_{0}|}\sqrt{4-{{x}_{0}}^{2}}$=$\frac{8\sqrt{2}}{|{y}_{0}|}|{y}_{0}|$=8$\sqrt{2}$.(为定值)
∴以MN为直径的圆必过圆O内的一定点(6-4$\sqrt{2}$,0).
点评 本题考查圆的方程的求法,考查以MN为直径的圆必过圆O内的一定点的证明,是中档题,解题时要认真审题,注意直线与圆的位置关系的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com