
分析 (1)由sin2α>0,确定α的正弦与余弦函数值的符号相同,根据余弦值小于0确定α的象限范围.
(2)先根据角的象限可以判定题中出现的sinθ、cosθ的值的范围,然后再根据sin(cosθ)•cos(sinθ)把内层的sinθ、cosθ看成弧度制表示的角即可判断符号.
解答 解:(1)∵sin2α>0,cosα<0,
∴2sinαcosα>0,
∴sinα<0,
∴α在第三、四象限
又∵cosα<0,
∴α在第三象限.
(2)∵θ是第三象限角,
∴-1<cosθ<0,-1<sinθ<0,即cosθ与sinθ可看成一个第四象限的角.
∴sin(cosθ)<0,cos(sinθ)>0.
∴sin(cosθ)•cos(sinθ)<0.
点评 本题考查象限角、轴线角,二倍角的正弦,考查分析问题解决问题的能力,是基础题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{9}$ | B. | $\frac{π}{9}$ | C. | $\frac{π}{18}$ | D. | $\frac{π}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1,1) | B. | (0,1,-3) | C. | (-1,0,3) | D. | (-1,0,-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
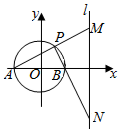 已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.
已知圆O的直径AB=4,定直线l到圆心的距离为6,且直线l⊥直线AB.点P是圆上异于A、B的任意一点,直线PA、PB分别交l于M、N点.如图,以AB为x轴,圆心O为原点建立平面直角坐标系xOy.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com