分析:(Ⅰ)欲证MN∥面ADD1A1,取CD的中点K,连接MK,NK,只需证面MNK∥面ADD1A1,根据面面平行的判定定理可知只需在一个平面内找两相交直线与另一平面平行,MK∥面ADD1A1,NK∥面ADD1A1,MN∩NK=N,满足定理条件.
(Ⅱ)设F为AD的中点,作FH⊥AE,交AE于H,连接PH,根据二面角的平面角的定义可知∠PHF为二面角P-AE-D的平面角,在Rt△PFH中求出此角即可.
解答:解:(Ⅰ)证明:取CD的中点K,连接MK,NK

∵M,N,K分别为AK,CD
1,CD的中点
∵MK∥AD,NK∥DD
1∴MK∥面ADD
1A
1,NK∥面ADD
1A
1∴面MNK∥面ADD
1A
1∴MN∥面ADD
1A
1(Ⅱ)设F为AD的中点
∵P为A
1D
1的中点∴PF∥DD
1∴PF⊥面ABCD
作FH⊥AE,交AE于H,连接PH,则由三垂线定理得AE⊥PH
从而∠PHF为二面角P-AE-D的平面角.
在Rt△AEF中,
AF=,EF=2a,AE=a,从而
FH===在Rt△PFH中,
tan∠PFH===故:二面角P-AE-D的大小为
arctan 点评:本小题主要考查长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力.

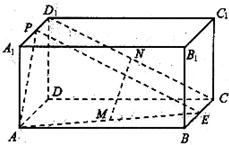



 19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 15、如图,长方体ABCD-A1B1C1D1中被截去一部分,
15、如图,长方体ABCD-A1B1C1D1中被截去一部分, 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点. 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )