【题目】已知函数
.
（1）判断
的单调性并写出证明过程；
（2）当
时，关于x的方程
在区间
上有唯一实数解，求a的取值范围.
【答案】（1）
在R上递增，证明见解析；（2）
或
.
【解析】
（1）先判断函数的奇偶性，再根据函数单调性的定义，作差比较大小即可求证明；
（2）根据（1）中所求单调性，将问题转化为
的零点问题，利用
之间的关系进行换元，转化为二次函数零点的分布问题即可求得.
（1）在R上递增.
证明：
，
恒成立，
的定义域为R.
令
，
，
是奇函数.
令
，
，
，
在
上递增，又
是R上连续不断的奇函数，
在R上递增.
（2）由（1）得
且在R上递增.
整理得
，在
上有唯一实数解
构造，，
.
令
，则
，
，
在
内有且只有一个零点，
无零点.
又
，
在
上为增函数.
ⅰ）若
在内有且只有一个零点，无零点.
则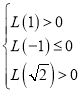
ⅱ）若
为的零点，无零点，
则
，
又，经检验符合题意.
综上所述：
或.
科目：高中数学 来源： 题型：
【题目】共享单车给市民出行带来了诸多便利，某公司购买了一批单车投放到某地给市民使用，
据市场分析，每辆单车的营运累计利润y（单位：元）与营运天数x
满足函数关系
式
.
（1）要使营运累计利润高于800元，求营运天数的取值范围；
（2）每辆单车营运多少天时，才能使每天的平均营运利润
的值最大？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P-ABCD中，AB//CD，且
（1）证明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC, 
,且四棱锥P-ABCD的体积为
，求该四棱锥的侧面积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
， (
为参数， 
为倾斜角).以坐标原点为极点， 
轴的正半轴为极轴建立极坐标系，曲线
的直角坐标方程为
.
（Ⅰ）将曲线
的直角坐标方程化为极坐标方程；
（Ⅱ）设点
的直角坐标为
，直线
与曲线
的交点为
、
，求
的取值范围.
【答案】（I）
；（II）
.
【解析】试题分析：（Ⅰ）将由
代入
，化简即可得到曲线
的极坐标方程；（Ⅱ）将
的参数方程
代入
，得
，根据直线参数方程的几何意义，利用韦达定理结合辅助角公式，由三角函数的有界性可得结果.
试题解析：（Ⅰ）由
及
，得
，即
所以曲线
的极坐标方程为
（II）将
的参数方程
代入
，得
∴
, 所以
，又
，
所以
，且
,
所以
,
由
，得
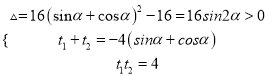，所以
.
故
的取值范围是
.
【题型】解答题
【结束】
23
【题目】已知
、
、
均为正实数.
（Ⅰ）若
，求证： 
（Ⅱ）若
，求证： 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知离心率为
的椭圆
焦点在
轴上，且椭圆
个顶点构成的四边形面积为
，过点
的直线
与椭圆
相交于不同的两点
、
.
（1）求椭圆
的方程；
（2）设
为椭圆上一点，且
（
为坐标原点）.求当
时，实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活，创建了社区“文化丹青”大型活动场所，配备了各种文化娱乐活动所需要的设施，让广大居民健康生活、积极向上．社区最近四年内在“文化丹青”上的投资金额统计数据如表：（为了便于计算，把2015年简记为5，其余以此类推）
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
（1）利用所给数据，求出投资金额
与年份
之间的回归直线方程
；
（2）预测该社区在2019年在“文化丹青”上的投资金额．
（附：对于一组数据
， 
，…， 
，其回归直线
的斜率和截距的最小二乘估计分别为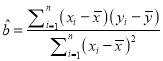
， 
．）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了展示中华汉字的无穷魅力，传递传统文化，提高学习热情，某校开展《中国汉字听写大会》的活动．为响应学校号召，2（9）班组建了兴趣班，根据甲、乙两人近期8次成绩画出茎叶图，如图所示（把频率当作概率）．
（1）求甲、乙两人成绩的平均数和中位数；
（2）现要从甲、乙两人中选派一人参加比赛，从统计学的角度，你认为派哪位学生参加比较合适？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
