
分析 (Ⅰ)求出θ的值,求出函数的单调区间,求出函数的极值即可;
(Ⅱ)构造F(x)=kx-$\frac{1}{x}$-lnx-$\frac{2e}{x}$=kx-$\frac{1+2e}{x}$-lnx,转化为:若在[1,e]上存在x1,使得F(x0)>0,求实数k的取值范围,由此利用分类讨论思想和导数性质能求出k的取值范围.
解答 解:(Ⅰ)f′(x)=-$\frac{1}{sinθ{•x}^{2}}$+$\frac{1}{x}$≥0在[1,+∞)上恒成立,即$\frac{sinθ•x-1}{sinθ{•x}^{2}}$≥0,
∵θ∈(0,π),∴sinθ>0,故sinθ•x-1≥0在[1,+∞)恒成立,
只需sinθ•1-1≥0,即sinθ≥1,又0<sinθ≤1只有sinθ=1得θ=$\frac{π}{2}$,
由f′(x)=$\frac{x-1}{{x}^{2}}$=0,解得:x=1,
故f(x)在(0,1)递减,在(1,+∞)递增,
故f(x)极小值=f(1)=1,无极大值;
(Ⅱ)构造F(x)=kx-$\frac{1}{x}$-lnx-$\frac{2e}{x}$=kx-$\frac{1+2e}{x}$-lnx,
则转化为:若在[1,e]上存在x1,使得F(x0)>0,求实数k的取值范围,
①当k≤0时,x∈[1,e],F(x)<0在[1,e]恒成立,
∴在[1,e]上不存在x0,使得kx0-f(x0)>$\frac{2e}{{x}_{0}}$成立.
②当k>0时,F′(x)=k+$\frac{1+2e}{{x}^{2}}$-$\frac{1}{x}$=$\frac{{kx}^{2}+1+e+(e-x)}{{x}^{2}}$,
∵x∈(1,e),∴e-x>0,
∴F′(x)>0在[1,e)恒成立,
故F(x)在[1,e]上单调递增,F(x)max=F(e)=ke-$\frac{1}{e}$-3,
只要ke-$\frac{1}{e}$-3>0,
解得k>$\frac{3e+1}{{e}^{2}}$.
综上,k的取值范围是($\frac{3e+1}{{e}^{2}}$,+∞).
点评 本题考查角的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | $6\sqrt{2}$ | B. | $\sqrt{2}+2\sqrt{5}$ | C. | $3\sqrt{2}$ | D. | $2\sqrt{2}+2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5+2$\sqrt{2}$] | B. | (-∞,8] | C. | [$\frac{26}{3}$,+∞) | D. | (-∞,5+2$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -sin(lnx) | B. | $\frac{sin(lnx)}{x}$ | C. | -$\frac{sin(lnx)}{x}$ | D. | $\frac{cos(lnx)}{x}$ |
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:选择题
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
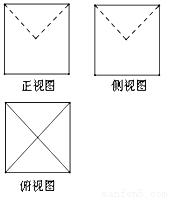
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com