
分析 (1)①、由对数的运算性质直接计算即可得答案;
②、由复数的计算性质,计算即可得答案;
(2)由导数的计算法则,直接计算即可得答案.
解答 解:根据题意,
(1)①、log327+lg25+lg4=3+lg(25×4)=3+2=5;
②、$\frac{{1-\sqrt{3}i}}{{(1+\sqrt{3}i{)^2}}}$=$\frac{1-\sqrt{3}i}{1-3+2\sqrt{3}i}$=$\frac{1-\sqrt{3}i}{-2+2\sqrt{3}i}$=-$\frac{1}{2}$;
(2)①f(x)=$\frac{1}{4}$x 4-$\frac{1}{3}$x 3+e x-3,其导数f′(x)=$\frac{1}{4}$×4x3-$\frac{1}{3}$×3x2+e x=x3-x2+e x,
②y=$\frac{sinx}{x}$,其导数y′=$\frac{(sinx)′x-sinx(x)′}{{x}^{2}}$=$\frac{x•cosx-sinx}{{x}^{2}}$.
点评 本题考查复数、对数函数以及函数导数的计算,关键是掌握计算的公式.


科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {-3,-1,0} | C. | {-1,0,2} | D. | {-3,0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
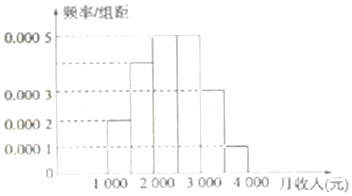
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:选择题
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com