
分析 问题转化为求直线l与圆x2+y2=22有公共点时,a的取值范围,利用数形结合思想能求出结果.
解答 解:∵直线l:x-y+a=0,点A(-2,0),B(2,0),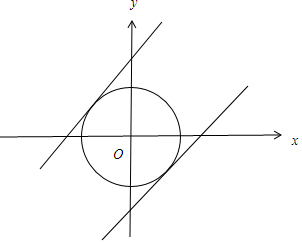
直线l上存在点P满足AB⊥BP,
∴如图,直线l与圆x2+y2=22有公共点,
∴圆心O(0,0)到直线l:x-y+a=0的距离:
d=$\frac{|a|}{\sqrt{2}}$≤2,
解得$-2\sqrt{2}≤a≤2\sqrt{2}$.
∴实数a的取值范围为[-2$\sqrt{2}$,2$\sqrt{2}$].
故答案为:[-2$\sqrt{2}$,2$\sqrt{2}$].
点评 本题考查实数的取值范围的求法,考查直线方程、圆、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,5+2$\sqrt{2}$] | B. | (-∞,8] | C. | [$\frac{26}{3}$,+∞) | D. | (-∞,5+2$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:选择题
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
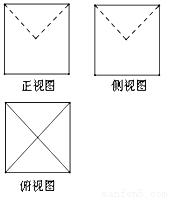
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系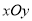 中,直线
中,直线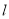 的参数方程为
的参数方程为 (
(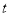 为参数),以原点
为参数),以原点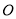 为极点,
为极点,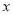 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线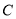 的极坐标方程为
的极坐标方程为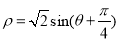 .
.
(1)求曲线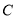 的直角坐标方程;
的直角坐标方程;
(2)若直线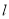 与曲线
与曲线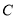 交于
交于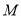 ,
,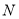 两点,求
两点,求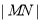 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com