
| A. | 48 | B. | 40 | C. | 32 | D. | 24 |
分析 求出椭圆的a,b,c,e,以及右准线方程,运用椭圆的第二定义,可得A的横坐标,求得纵坐标,再由三角形的面积公式,计算即可得到所求值.
解答 解:椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1中a=7,b=2$\sqrt{6}$,c=$\sqrt{49-24}$=5,
e=$\frac{c}{a}$=$\frac{5}{7}$,右准线方程为x=$\frac{49}{5}$,
|AF2|=ed=e($\frac{{a}^{2}}{c}$-xA)=a-exA=6,
即为7-$\frac{5}{7}$xA=6,可得xA=$\frac{7}{5}$,
yA=±$\sqrt{24(1-\frac{1}{25})}$=±$\frac{24}{5}$,
则△AF1F2的面积是$\frac{1}{2}$•2c•|yA|
=5•$\frac{24}{5}$=24.
故选:D.
点评 本题考查椭圆的方程和性质,考查焦半径公式的运用,以及三角形的面积的求法,考查运算能力,属于基础题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}+\frac{y^2}{{\frac{81}{4}}}$=1 | B. | $\frac{x^2}{4}+\frac{y^2}{9}$=1 | C. | $\frac{x^2}{{\frac{81}{4}}}+\frac{y^2}{9}$=1 | D. | $\frac{x^2}{9}+\frac{y^2}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
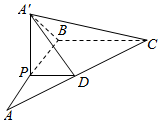 如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.
如图,在△ABC中,∠B=$\frac{π}{2}$,AB=BC=2,P为AB上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA′,使平面PDA′⊥平面PBCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.
一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
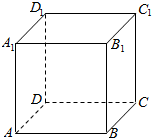 (A类题)如图,在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1,C1,B,D,若A1,C1,B,D四个点都在同一球面上,则该球的表面积为3π.
(A类题)如图,在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1,C1,B,D,若A1,C1,B,D四个点都在同一球面上,则该球的表面积为3π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com