
 一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.
一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.分析 (Ⅰ)由频率=$\frac{频数}{样本容量}$,利用频率和为1,即可求出a、b的值;
(Ⅱ)利用频率分布直方图中中位数两侧的频率相等,列出方程求出中位数x;
(Ⅲ)求出这20棵果树产量的平均数$\overline{x}$,用样本数据估计总体的产量即可.
解答 解:(Ⅰ)由样本中产量在区间(45,50]上的果树棵数为8,
得a×5×20=8,解得a=0.08;
又因为5×(0.06+0.08+b+0.02)=1,
解得b=0.04,
所以a=0.08,b=0.04;
(Ⅱ)设这20棵果树产量的中位数为x,
因为样本中产量在区间(40,45]上的频率为0.06×5=0.03,
样本中产量在区间(45,50]上的频率为0.08×5=0.4,
所以中位数在区间(45,50]内,
令0.06×5+(x-45)×0.08=0.5,
解得x=47.5,
所以估计这20棵果树产量的中位数为47.5;
(Ⅲ)设这20棵果树产量的平均数是$\overline{x}$,
则$\overline{x}$=5×(42.5×0.06+47.5×0.08+52.5×0.04+57.5×0.02)=48(kg);
根据样本数据估计这1000棵果树的总产量为48×1000=48000(kg).
点评 本题考查了频率分布直方图的应用问题,也考查了频率、中位数与平均数的计算问题,是基础题目.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
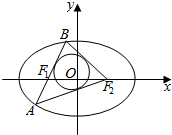 如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.
如图,设椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 40 | C. | 32 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (0,2) | C. | (-2,2) | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| X | 0 | 1 | 2 |
| P | a | b | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com