
分析 (1)由正弦定理化简已知等式可得:(2sinB-sinA)cosC=sinCcosA,利用三角形内角和定理整理可得2sinBcosC=sinB,由sinB≠0,解得cosC=$\frac{1}{2}$,结合范围0<C<π,可求C的值.
(2)设△ABC外接圆的半径为R 由题意得2R=$\frac{c}{sinC}=\frac{3}{{sin\frac{π}{3}}}$=2$\sqrt{3}$,由sinA+sinB=2$\sqrt{6}$sinAsinB得a+b=$\sqrt{2}$ab,由余弦定理得(a+b)-3ab-9=0,联立解得ab的值,利用三角形面积公式即可得解.
解答 解:(1)由于(2b-a )cosC=ccosA,由正弦定理得(2sinB-sinA)cosC=sinCcosA,
即2sinBcosC=sinAcosC+sinCcosA,即2sinBcosC=sin(A+C),可得:2sinBcosC=sinB,
因为sinB≠0,所以cosC=$\frac{1}{2}$,
因为0<C<π,所以C=$\frac{π}{3}$.
(2)设△ABC外接圆的半径为R 由题意得2R=$\frac{c}{sinC}=\frac{3}{{sin\frac{π}{3}}}$=2$\sqrt{3}$,
由sinA+sinB=2$\sqrt{6}$sinAsinB得,2R(a+b)=2$\sqrt{6}$ab,即a+b=$\sqrt{2}$ab,①
由余弦定理得,a2+b2-ab=9,即(a+b)-3ab-9=0,②
将①式代入②得2(ab)2-3ab-9=0,解得 ab=3或ab=-$\frac{3}{2}$(舍去),
所以S△ABC=$\frac{1}{2}$absinC=$\frac{{3\sqrt{3}}}{4}$.
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式,余弦函数的图象和性质在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.
一果农种植了1000棵果树,为估计其产量,从中随机选取20棵果树的产量(单位:kg)作为样本数据,得到如图所示的频率分布直方图.已知样本中产量在区间(45,50]上的果树棵数为8,.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
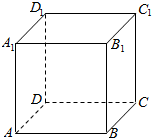 (A类题)如图,在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1,C1,B,D,若A1,C1,B,D四个点都在同一球面上,则该球的表面积为3π.
(A类题)如图,在棱长为1的正方形ABCD-A1B1C1D1中选取四个点A1,C1,B,D,若A1,C1,B,D四个点都在同一球面上,则该球的表面积为3π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
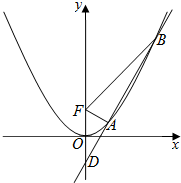 已知抛物线C:x2=4y的焦点为F,过点D(0,-1)的直线l与抛物线C交于不同的A、B两点.
已知抛物线C:x2=4y的焦点为F,过点D(0,-1)的直线l与抛物线C交于不同的A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com