
分析 利用平面向量的数量积化简求解即可.
解答 解:模为2的向量$\overrightarrow a$与单位向量$\overrightarrow b$的夹角为$\frac{2π}{3}$,可得$|\overrightarrow{a}|=2$,$|\overrightarrow{b}|=1$,cos$\frac{2π}{3}$=$-\frac{1}{2}$
则$(2\overrightarrow a-\overrightarrow b)•(\overrightarrow a+\overrightarrow b)$=2${\overrightarrow{a}}^{2}$+$\overrightarrow{a}•\overrightarrow{b}$-${\overrightarrow{b}}^{2}$=8+2×$1×(-\frac{1}{2})$-1=6.
故答案为:6.
点评 本题考查向量的数量积的应用,考查计算能力.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$| | B. | $\frac{1}{2}$$|\begin{array}{l}{{x}_{1}}&{{y}_{1}}&{1}\\{{x}_{2}}&{{y}_{2}}&{1}\\{{x}_{3}}&{{y}_{3}}&{1}\end{array}|$ | ||
| C. | $\frac{1}{2}$|$\overrightarrow{AB}$$•\overrightarrow{AC}$| | D. | $\frac{1}{2}$(cos|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
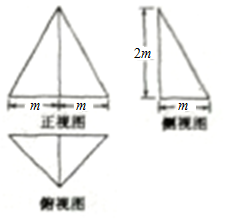 一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )
一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )| A. | $36\sqrt{3}$ | B. | $\frac{98}{3}$ | C. | $\frac{116}{3}$ | D. | $\frac{128}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a+b}{2}$ | B. | $\sqrt{ab}$ | C. | $\sqrt{\frac{{{a^2}+{b^2}}}{2}}$ | D. | $\frac{ab}{a+b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(1)≤1成立,则f(9)≤81成立 | |
| B. | 若f(2)≤4成立,则f(1)>1成立 | |
| C. | 若f(3)>9成立,则当k≥1时,均有f(k)>k2成立 | |
| D. | 若f(3)>16成立,则当k≥3时,均有f(k)>k2成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com