
分析 利用两个向量的数量积的定义和公式,向量的模的定义,以及一个向量在另一个向量上的投影的定义,得出结论.
解答 解:∵O是坐标原点,A(2,-1),B(-4,8),
∴(1)$\overrightarrow{AB}$=(-6,9),|$\overrightarrow{AB}$|=$\sqrt{{(-6)}^{2}{+9}^{2}}$=$\sqrt{117}$.
(2)与$\overrightarrow{AB}$平行的单位向量为$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$=($\frac{-6}{\sqrt{117}}$,$\frac{9}{\sqrt{117}}$)=(-$\frac{2}{\sqrt{13}}$,$\frac{3}{\sqrt{13}}$),或-$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$=($\frac{2}{\sqrt{13}}$,-$\frac{3}{\sqrt{13}}$).
(3)求与$\overrightarrow{AB}$平行且模长为2的向量为2•$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$=(-$\frac{36}{\sqrt{117}}$,$\frac{18}{\sqrt{117}}$)=(-$\frac{12}{\sqrt{13}}$,$\frac{6}{\sqrt{13}}$),或-2•$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$=($\frac{12}{\sqrt{13}}$,-$\frac{6}{\sqrt{13}}$).
(4)∵$\overrightarrow{m}$=(9,6)满足$\overrightarrow{m}•\overrightarrow{AB}$=0,∴$\overrightarrow{m}$⊥$\overrightarrow{AB}$,
故与$\overrightarrow{AB}$垂直的单位向量为$\frac{\overrightarrow{m}}{|\overrightarrow{m}|}$=($\frac{9}{\sqrt{117}}$,$\frac{6}{\sqrt{117}}$)=($\frac{3}{\sqrt{13}}$,$\frac{2}{\sqrt{13}}$),或-$\frac{\overrightarrow{m}}{|\overrightarrow{m}|}$=(-$\frac{3}{\sqrt{13}}$,-$\frac{2}{\sqrt{13}}$).
(5)由(4)可得,与$\overrightarrow{AB}$垂直且模长为2的向量为2$\frac{\overrightarrow{m}}{|\overrightarrow{m}|}$=($\frac{18}{\sqrt{117}}$,$\frac{12}{\sqrt{117}}$)=($\frac{6}{\sqrt{13}}$,$\frac{4}{\sqrt{13}}$),或为-2$\frac{\overrightarrow{m}}{|\overrightarrow{m}|}$=(-$\frac{6}{\sqrt{13}}$,-$\frac{4}{\sqrt{13}}$).
(6)$\overrightarrow{OA}$$•\overrightarrow{OB}$=(2,-1)•(-4,8)=-8+(-8)=-16.
(7)设$\overrightarrow{OA}$在$\overrightarrow{OB}$上的射影为n,∵$\overrightarrow{OA}$$•\overrightarrow{OB}$=n•|$\overrightarrow{OB}$|=n•$\sqrt{16+64}$=-16,∴n=-$\frac{4\sqrt{5}}{5}$.
(8)设$\overrightarrow{OB}$在$\overrightarrow{OA}$上的射影k,∵$\overrightarrow{OA}$$•\overrightarrow{OB}$=k•|$\overrightarrow{OA}$|=k•$\sqrt{5}$=-16,∴k=-$\frac{16\sqrt{5}}{5}$.
(9)设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,∵$\overrightarrow{OA}$$•\overrightarrow{OB}$=|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•cosθ=$\sqrt{5}$•$\sqrt{80}$•cosθ=-16,
∴cosθ=-$\frac{4}{5}$,∴θ=π-arcos$\frac{4}{5}$.
点评 本题主要考查两个向量的数量积的运算,求向量的模,一个向量在另一个向量上的投影,属于中档题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
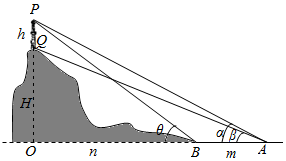 如图,勘探队员朝一座山行进,在前后两处A,B观察塔尖P及山顶Q,己知A,B,O在同一水平面,P,Q,A,B,O在同一平面且与水平面垂直.
如图,勘探队员朝一座山行进,在前后两处A,B观察塔尖P及山顶Q,己知A,B,O在同一水平面,P,Q,A,B,O在同一平面且与水平面垂直.查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:解答题
设 为虚数单位,
为虚数单位,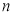 为正整数,
为正整数,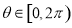 .
.
(1)用数学归纳法证明: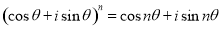 ;
;
(2)已知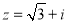 ,试利用(1)的结论计算
,试利用(1)的结论计算 ;
;
(3)设复数 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 2或1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com