
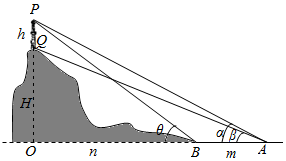
 如图,勘探队员朝一座山行进,在前后两处A,B观察塔尖P及山顶Q,己知A,B,O在同一水平面,P,Q,A,B,O在同一平面且与水平面垂直.
如图,勘探队员朝一座山行进,在前后两处A,B观察塔尖P及山顶Q,己知A,B,O在同一水平面,P,Q,A,B,O在同一平面且与水平面垂直.分析 (I)在△PAB中使用正弦定理得出h;
(II)根据锐角三角函数的定义用m,n表示出H,H+h,n,即可得出h.
解答 解:(I)在△ABP中,∠APB=∠PBO-∠PAO=θ-α,
由正弦定理得:$\frac{h}{sinα}=\frac{m}{sin(θ-α)}$,
解得h=$\frac{msinα}{sin(θ-α)}$.
(II)连结QB.
∵tanα=$\frac{H+h}{m+n}$,tanθ=$\frac{H+h}{n}$,
∴(m+n)tanα=ntanθ,
∴n=$\frac{mtanα}{tanθ-tanα}$.
∴H+h=ntanθ=$\frac{mtanαtanθ}{tanθ-tanα}$.
又tanω=$\frac{H}{n}$,∴H=ntanω=$\frac{mtanαtanω}{tanθ-tanα}$.
∴h=$\frac{mtanαtanθ}{tanθ-tanα}$-$\frac{mtanαtanω}{tanθ-tanα}$=$\frac{mtanα(tanθ-tanω)}{tanθ-tanα}$.
点评 本题考查了解三角形的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | [-2,0) | C. | ∅ | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8x+16y+3=0 | B. | 8x-16y+3=0 | C. | 16x+8y+3=0 | D. | 16x-8y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | -$\frac{5}{13}$ | C. | $±\frac{12}{13}$ | D. | ±$\frac{5}{13}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(理)试卷(解析版) 题型:填空题
若集合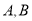 满足
满足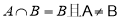 ,则命题“
,则命题“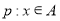 ”是命题“
”是命题“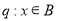 ”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com