
| A. | 8x+16y+3=0 | B. | 8x-16y+3=0 | C. | 16x+8y+3=0 | D. | 16x-8y+3=0 |
分析 求出原函数的导函数,设出切点,得到函数在切点处的导数,求出切点坐标,再由直线方程的点斜式得答案.
解答 解:由y=x4,得y′=4x3,
设切点坐标为(x0,y0),则$y′{|}_{x={x}_{0}}=4{{x}_{0}}^{3}$,
∵切线l与直线x+2y-8=0平行,∴$4{{x}_{0}}^{3}=-\frac{1}{2}$,解得${x}_{0}=-\frac{1}{2}$.
∴${y}_{0}={{x}_{0}}^{4}=\frac{1}{16}$,
∴直线l的方程为y-$\frac{1}{16}=-\frac{1}{2}(x+\frac{1}{2})$,即8x+16y+3=0.
故选:A.
点评 本题考查利用导数研究过曲线上某点处的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
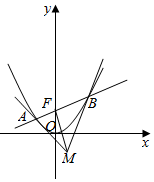 如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.
如图,已知F是抛物线x2=2py(p>0)的焦点,O为坐标原点,过点O、F的圆的圆心为Q,点Q到抛物线准线的距离为$\frac{3}{2}$.过点F的直线l交抛物线于A,B两点,过A,B分别作抛物线的切线,两切线交点为M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
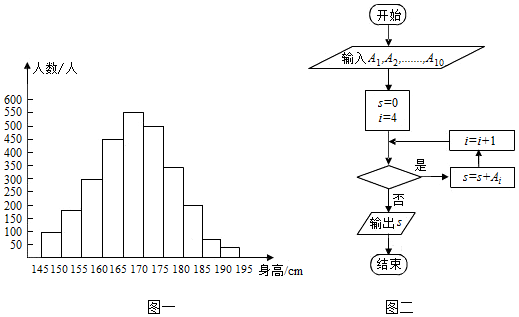
| A. | i<6?,1000 | B. | i<7?,1500 | C. | i<8?,1850 | D. | i<9?,2050 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
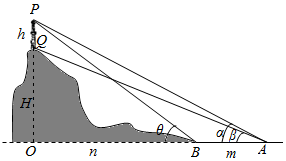 如图,勘探队员朝一座山行进,在前后两处A,B观察塔尖P及山顶Q,己知A,B,O在同一水平面,P,Q,A,B,O在同一平面且与水平面垂直.
如图,勘探队员朝一座山行进,在前后两处A,B观察塔尖P及山顶Q,己知A,B,O在同一水平面,P,Q,A,B,O在同一平面且与水平面垂直.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -log20152014 | B. | 1 | C. | -1+log20152014 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com