
| A. | -log20152014 | B. | 1 | C. | -1+log20152014 | D. | -1 |
分析 要求log2015x1+log2015x2+…+log2015x2014,需求x1•x2•…•x2014的值,只须求出切线与x轴的交点的横坐标即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
解答 解:对y=xn+1(n∈N*)求导,得y′=(n+1)xn,
令x=1得在点(1,1)处的切线的斜率k=n+1,在点
(1,1)处的切线方程为y-1=k(xn-1)=(n+1)(xn-1),
不妨设y=0,可得xn=$\frac{n}{n+1}$,
则x1•x2•x3…•xn=$\frac{1}{2}$•$\frac{2}{3}$•$\frac{3}{4}$…•$\frac{n}{n+1}$=$\frac{1}{n+1}$,
从而log2015x1+log2015x2+…+log2015x2014
=log2015(x1•x2…x2014)
=log2015$\frac{1}{2015}$=-1..
故选:D.
点评 本题主要考查直线的斜率、利用导数研究曲线上某点切线方程、数列等基础知识,考查运算求解能力、化归与转化思想.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 8x+16y+3=0 | B. | 8x-16y+3=0 | C. | 16x+8y+3=0 | D. | 16x-8y+3=0 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:解答题
已知函数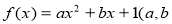 为实数),设
为实数),设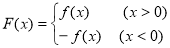
(1)若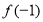 = 0且对任意实数
= 0且对任意实数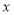 均有
均有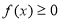 成立,求
成立,求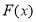 表达式;
表达式;
(2)在(1)的条件下,当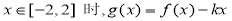 是单调函数,求实数
是单调函数,求实数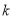 的取值范围;
的取值范围;
(3)设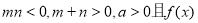 满足
满足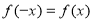 ,试比较
,试比较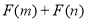 的值与0的大小.
的值与0的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π2a3 | B. | π2a3 | C. | $\frac{{π}^{2}}{2}$a3 | D. | $\frac{{π}^{2}}{3}$a3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com