
分析 (1)根据已知直线l的解析式可以求得直线l的斜率为$\frac{1}{2}$,然后设所求直线为点斜式,利用待定系数法解答即可;
(2)根据已知直线l的解析式可以求得直线l的斜率为-2,然后设所求直线为点斜式,利用待定系数法解答即可.
解答 解:(1)因为两直线互相平行,且${k_l}=\frac{1}{2}$,所以所求直线的斜率为$\frac{1}{2}$,
故所求直线的方程$y-1=\frac{1}{2}(x-2)$,即x-2y=0;
(2)因为两直线互相垂直,所以所求直线的斜率为-2,
故所求直线的方程y-1=-2(x-2),即2x+y-5=0.
点评 本题主要考查利用两直线平行、垂直的性质,用待定系数法求直线方程,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | sinα | C. | -tanα | D. | tanα |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
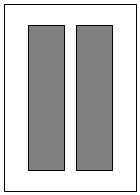 如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm
如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com