
分析 作出曲线(x-1)(y-1)=-1的图象,由题意可得|x-2y|即为曲线上任一点到直线x-2y=0的距离的$\sqrt{5}$倍的最小值.
可得与曲线相切,且与直线x-2y=0平行的直线距离的$\sqrt{5}$倍,求出函数的导数,求出切线的斜率,求得切点,代入即可得到所求最小值.
解答  解:实数x,y满足x+y-xy≥2,
解:实数x,y满足x+y-xy≥2,
即为(x-1)(y-1)≤-1,
作出曲线(x-1)(y-1)=-1的图象,
由题意可得|x-2y|即为
曲线上任一点到直线x-2y=0的距离的$\sqrt{5}$倍的最小值.
可得与曲线相切,且与直线x-2y=0平行的直线距离的$\sqrt{5}$倍.
设切点为(m,n),由y=1-$\frac{1}{x-1}$的导数为y′=$\frac{1}{(x-1)^{2}}$,
即有切线的斜率为$\frac{1}{(m-1)^{2}}$=$\frac{1}{2}$,
解得m=1+$\sqrt{2}$(负的舍去),
切点为(1+$\sqrt{2}$,1-$\frac{\sqrt{2}}{2}$),
则|x-2y|的最小值为|1+$\sqrt{2}$-2(1-$\frac{\sqrt{2}}{2}$)|=2$\sqrt{2}$-1.
故答案为:2$\sqrt{2}$-1.
点评 本题考查最值的求法,注意运用导数求得切点,考查化简整理的运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如表:
今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如表:| 年龄(岁) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] |
| 频数 | m | n | 14 | 12 | 8 | 6 |
| 知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
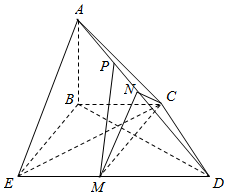 如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,AB=3.M,N分别为DE,AD的中点.
如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,AB=3.M,N分别为DE,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com