练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

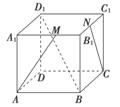
    如图所示，正方体ABCD－A1B1C1D1中，M、N分别是A1B1、B1C1的中点．问：

    (1)AM和CN是否是异面直线？说明理由；

    (2)D1B和CC1是否是异面直线？说明理由．


    解：

    (1)不是异面直线．理由如下：

    连接MN、A1C1、AC.

    ∵M、N分别是A1B1、B1C1的中点，

    ∴MN∥A1C1.

    又∵A1A綊C1C，

    ∴A1ACC1为平行四边形，

    ∴A1C1∥AC，∴MN∥AC，

    ∴A、M、N、C在同一平面内，故AM和CN不是异面直线．

    (2)是异面直线．证明如下：

    ∵ABCD－A1B1C1D1是正方体，

    ∴B、C、C1、D1不共面．

    假设D1B与CC1不是异面直线，

    则存在平面α，使D1B⊂平面α，CC1⊂平面α，

    ∴D1、B、C、C1∈α，与ABCD－A1B1C1D1是正方体矛盾．

    ∴假设不成立，即D1B与CC1是异面直线．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在Rt△ABC中，AB⊥AC，AD⊥BC于D，求证：，那么在四面体A－BCD中，类比上述结论，你能得到怎样的猜想？并说明理由．

    图①

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在一个几何体的三视图中，主视图和俯视图如图所示，则相应的左视图可以为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在长方体ABCD－A1B1C1D1中，AB＝AD＝3 cm，AA1＝2 cm，则四棱锥A－BB1D1D的体积为________cm3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设P表示一个点，a，b表示两条直线，α，β表示两个平面，给出下列四个命题，其中正确的命题是(　　)

    ①P∈a，P∈α⇒a⊂α；

    ②a∩b＝P，b⊂β⇒a⊂β；

    ③a∥b，a⊂α，P∈b，P∈α⇒b⊂α；

    ④α∩β＝b，P∈α，P∈β⇒P∈b.

    A．①②                           B．②③

    C．①④                           D．③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，等腰直角三角形ABC中，∠A＝90°，BC＝，DA⊥AC，DA⊥AB，若DA＝1，且E为DA的中点．求异面直线BE与CD所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    考查下列两个命题，在“________”处都缺少同一个条件，补上这个条件使其构成真命题(其中a、b为不同的直线，α、β为不重合的平面)，则此条件为________．

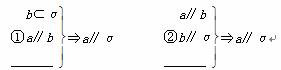
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    (2011·高考课标全国卷)如图，四棱锥P－ABCD中，底面ABCD为平行四边形，∠DAB＝60°，AB＝2AD，PD⊥底面ABCD.

    (1)证明：PA⊥BD；

    (2)设PD＝AD＝1，求棱锥D－PBC的高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列说法中正确的个数是(　　)

    ①总体中的个体数不多时宜用简单随机抽样法；

    ②在总体均分后的每一部分进行抽样时，采用的是简单随机抽样；

    ③百货商场的抓奖活动是抽签法；

    ④整个抽样过程中，每个个体被抽取的概率相等(有剔除时例外)．

    A．1                              B．2

    C．3                              D．4

    查看答案和解析>>

    同步练习册答案