
在Rt△AB C中,AB⊥AC,AD⊥BC于D,求证:
C中,AB⊥AC,AD⊥BC于D,求证: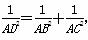 ,那么在四面体A-BCD中,类比上述结论,你能得到怎样的猜想?并说明理由.
,那么在四面体A-BCD中,类比上述结论,你能得到怎样的猜想?并说明理由.
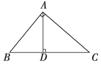
图①
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
已知二次函数f(x)的二次项系数为a,且不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
记Sn是等差数列{an}前n项的和,Tn是等比数列{bn}前n项的积,设等差数列{ an}公差d≠0,若对小于2013的正整数n,都有Sn=S2013-n成立,则推导出a1007=0,设等比数列{bn}的公比q≠1,若对于小于23的正整数n,都有 Tn=T23-n成立,则( )
an}公差d≠0,若对小于2013的正整数n,都有Sn=S2013-n成立,则推导出a1007=0,设等比数列{bn}的公比q≠1,若对于小于23的正整数n,都有 Tn=T23-n成立,则( )
A.b11=1 B.b12=1
C.b13= 1 D.b14=1
1 D.b14=1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题:“若数列{an}是等比数列,且an>0,则数列bn=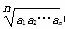 (n∈N*)也是等比数列”.类比这一性质,你能得到关于等差数列的一个什么性质?并证
(n∈N*)也是等比数列”.类比这一性质,你能得到关于等差数列的一个什么性质?并证 明你的结论.
明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
设a,b是两个实数,给出下列条件:
①a+b>1;②a+b=2;③a+b>2;④a2+b2>2;⑤ab>1.其中能推出:“a,b中至 少有一个大于1”的条件是( )
少有一个大于1”的条件是( )
A.②③ B.①②③
C.③ D.③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1、B1C1的中点.问:
(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.
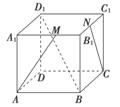
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com