练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    记Sn是等差数列{an}前n项的和，Tn是等比数列{bn}前n项的积，设等差数列{an}公差d≠0，若对小于2013的正整数n，都有Sn＝S2013－n成立，则推导出a1007＝0，设等比数列{bn}的公比q≠1，若对于小于23的正整数n，都有 Tn＝T23－n成立，则(　　)

    A．b11＝1                       B．b12＝1

    C．b13＝1                       D．b14＝1


    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在如下数表中，已知每行、每列中的数都成等差数列，

    那么位于表中的第n行第n＋1列的数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式x2＋ax＋4＜0的解集不是空集，则实数a的取值范围是(　　)

    A．－4≤a≤4                      B．－4＜a＜4

    C．a≥4或a≤－4                  D．a＜－4或a＞4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知O是坐标原点，点A(－1,1)，若点M(x，y)为平面区域上的一个动点，则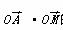的取值范围是(　　)

    A．[－1,0]                           B．[0,1]

    C．[0,2]                             D．[－1,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果实数x，y满足，目标函数z＝kx＋y的最大值为12，最小值为3，那么实数k的值为(　　)

    A．2                                 B．－2

    C.                                D．不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    回文数是指从左到右读与从右到左读都一样的正整数，如22,121,3443,94249等．显然2位回文数有9个：11,22,33，…，99.3位回文数有90个：101,111,121，…，191,202，…999.则

    (1)4位回文数有________个；

    (2)2n＋1(n∈N＋)位回文数有________个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在Rt△ABC中，AB⊥AC，AD⊥BC于D，求证：，那么在四面体A－BCD中，类比上述结论，你能得到怎样的猜想？并说明理由．

    图①

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某个与正整数n有关的命题，如果当n＝k(k∈N＋，k≥1)时，该命题成立，则一定可推得当n＝k＋1时，该命题也成立，现已知n＝5时，该命题不成立，则有(　　)

    A．当n＝4时，该命题成立

    B．当n＝6时，该命题成立

    C．当n＝4时，该命题不成立

    D．当n＝6时，该命题不成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在长方体ABCD－A1B1C1D1中，AB＝AD＝3 cm，AA1＝2 cm，则四棱锥A－BB1D1D的体积为________cm3.

    查看答案和解析>>

    同步练习册答案