练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在长方体ABCD－A1B1C1D1中，AB＝AD＝3 cm，AA1＝2 cm，则四棱锥A－BB1D1D的体积为________cm3.


    6


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    记Sn是等差数列{an}前n项的和，Tn是等比数列{bn}前n项的积，设等差数列{an}公差d≠0，若对小于2013的正整数n，都有Sn＝S2013－n成立，则推导出a1007＝0，设等比数列{bn}的公比q≠1，若对于小于23的正整数n，都有 Tn＝T23－n成立，则(　　)

    A．b11＝1                       B．b12＝1

    C．b13＝1                       D．b14＝1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明“对于足够大的自然数n，总有2n＞n2”时，验证第一步不等式成立所取的第一个值n0最小应当是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若某空间几何体的三视图如图所示，则该几何体的体积是(　　)

    A.　　　　　　　　　　　　      B.

    C．1                              D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    以圆柱的下底面为底面，并以圆柱的上底面圆心为顶点作圆锥，则该圆锥与圆柱等底等高．若圆锥的轴截面是一个正三角形，则圆柱的侧面积与圆锥的侧面积之比为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体ABCD－A1B1C1D1中，过顶点A1与正方体其他顶点的连线与直线BC1成60°角的条数为(　　)

    A．1                              B．2

    C．3                              D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


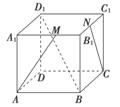
    如图所示，正方体ABCD－A1B1C1D1中，M、N分别是A1B1、B1C1的中点．问：

    (1)AM和CN是否是异面直线？说明理由；

    (2)D1B和CC1是否是异面直线？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列命题中，是假命题的是(　　)

    A．三角形的两条边平行于一个平面，则第三边也平行于这个平面

    B．平面α∥平面β，a⊂α，过β内的一点B有唯一的一条直线b，使b∥a

    C．α∥β，γ∥δ，α、β与γ、δ的交线分别为a、b、c、d，则a∥b∥c∥d

    D．一条直线与两个平面成等角是这两个平面平行的充要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，已知正三棱柱ABC－A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD与平面B1DC所成角的正弦值为________．

    查看答案和解析>>

    同步练习册答案