Question

3．已知线段AB的长为2，动点C满足$\overrightarrow{CA}$•$\overrightarrow{CB}$=λ（λ为负常数），且点C总不在以点B为圆心，$\frac{1}{2}$为半径的圆内，则实数λ的最大值是-$\frac{3}{4}$．

Answer 1

分析 由题意建立坐标系，假设点C在圆内，B（0，0），A（2，0），C（rcosa，rsina），（r＜$\frac{1}{2}$），从而利用坐标表示出向量，从而可得λ=-2rcosa+r²，从而求得．

解答 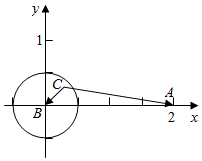解：由题意建立坐标系如右图，
假设点C在圆内，
则B（0，0），A（2，0），C（rcosa，rsina），（r＜$\frac{1}{2}$），
则$\overrightarrow{CA}$=（2-rcosa，-rsina），$\overrightarrow{CB}$=（-rcosa，-rsina），
∴λ=（2-rcosa，-rsina）•（-rcosa，-rsina）
=-2rcosa+r²（cos²a+sin²a）
=-2rcosa+r²，
∴r²-2r≤λ≤r²+2r，
故-$\frac{3}{4}$＜λ＜$\frac{5}{4}$，
∵点C总不在以点B为圆心，$\frac{1}{2}$为半径的圆内，
∴λ≤-$\frac{3}{4}$或λ≥$\frac{5}{4}$（舍）；
故实数λ的最大值是-$\frac{3}{4}$，
故答案为：-$\frac{3}{4}$．

点评 本题考查了平面向量的坐标表示的应用及数量积的求法，同时考查了数形结合的思想与转化思想的应用．