
分析 由题意可得A≤x,A≤$\frac{y}{{x}^{2}+{y}^{2}}$,运用不等式的可乘性和重要不等式a2+b2≥2ab,(a=b取得等号),即可得到A的最大值.
解答 解:A=min(x,$\frac{y}{{x}^{2}+{y}^{2}}$),
可得A≤x,A≤$\frac{y}{{x}^{2}+{y}^{2}}$,
由x,y>0,可得A2≤$\frac{xy}{{x}^{2}+{y}^{2}}$,
又x2+y2≥2xy,当且仅当x=y取得等号.
即有$\frac{xy}{{x}^{2}+{y}^{2}}$≤$\frac{1}{2}$,
则A2≤$\frac{1}{2}$,即A≤$\frac{\sqrt{2}}{2}$.
则A的最大值为$\frac{\sqrt{2}}{2}$.
点评 本题考查新定义的理解和运用,考查最值的求法,注意运用基本不等式和不等式的传递性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
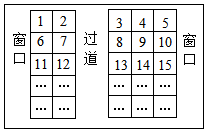 两同学预定春节返程票,希望两座相连,且有一人靠窗,从网上看余票尚有(48,49)、(62,63)、(75,76)、(84,85)四组,硬座车厢的座位号设置如图所示,那么他们应该订购的座位号是(84,85).
两同学预定春节返程票,希望两座相连,且有一人靠窗,从网上看余票尚有(48,49)、(62,63)、(75,76)、(84,85)四组,硬座车厢的座位号设置如图所示,那么他们应该订购的座位号是(84,85).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题①,②均为真命题 | B. | 命题②,③均为假命题 | ||
| C. | 命题②,④均为假命题 | D. | 命题①,③,④均为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com