练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知实数x，y满足x2+y2-4x+2=0，则x2+（y-2）2的最小值是（　　）
    A．$\sqrt{2}$B．$2\sqrt{2}$C．2D．8

    分析 x2+（y-2）2表示圆x2+y2-4x+2=0上动点（x，y）到点（0，2）点的距离的平方，进而得到答案．

    解答 解：x2+y2-4x+2=0表示一个以（2，0）点为圆心，以$\sqrt{2}$为半径的圆，
    x2+（y-2）2表示圆上动点（x，y）到点（0，2）点的距离的平方，
    故x2+（y-2）2的最小值是[$\sqrt{（0-2）^{2}+（2-0）^{2}}$-$\sqrt{2}$]2=2，
    故选：C．

    点评 本题考查的知识点是圆的一般方程，点到圆上动点距离的最值，两点之间的距离公式，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．极坐标系与直角坐标系xOy有相同的长度单位，以原点O为极点，以x轴正半轴为极轴．已知直线l的参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=\sqrt{3}t}\end{array}\right.$（t为参数），曲线C的极坐标方程为ρsin2θ=8cosθ．
    （1）求C的直角坐标方程；
    （2）设直线l与曲线C交于A，B两点，求弦长|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．如图，在△ABC中，点D在边AB上，CD⊥BC，AC=5$\sqrt{3}$，CD=5，BD=2AD．
    （Ⅰ）求AD的长；
    （Ⅱ）求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设0＜a＜1，实数x，y满足$|x|-{log_a}\frac{1}{y}=0$，则y关于x的函数的图象形状大致是（　　）
    A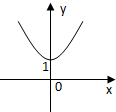．B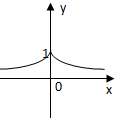．C．D．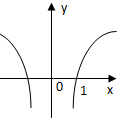

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．下列函数在定义域上为增函数的是（　　）
    A．y=x3B．$y=-\frac{1}{x}$C．$y={log_{\frac{1}{2}}}$xD．$y={（\frac{1}{2}）^x}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．为了解荆州中学学生健康状况，从去年高二年级体检表中抽取若干份，将他们的体重数据作为样本．将样本的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．
    （Ⅰ）求样本的容量；
    （Ⅱ）以荆州中学的样本数据来估计全省的总体数据，若从全省高二年级的所有学生中（人数很多）任选三人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知|$\overrightarrow{a}$|=2|$\overrightarrow{b}$|≠0，且$\overrightarrow{b}$⊥（$\overrightarrow{a}$-$\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是（　　）
    A．$\frac{π}{4}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{3π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．设f（x）=3x2ex，则f′（2）=（　　）
    A．12eB．12e2C．24eD．24e2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知平面内两点M（2，-2），N（4，4）．
    （Ⅰ）求MN的中垂线方程；
    （Ⅱ）求过点P（2，-3）且与直线MN平行的直线l的方程．

    查看答案和解析>>

    同步练习册答案