
 Ϊ�˽⾣����ѧѧ������״������ȥ��߶��꼶�����г�ȡ���ɷݣ������ǵ�����������Ϊ����������������������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3�����е�2С���Ƶ��Ϊ12��
Ϊ�˽⾣����ѧѧ������״������ȥ��߶��꼶�����г�ȡ���ɷݣ������ǵ�����������Ϊ����������������������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3�����е�2С���Ƶ��Ϊ12������ �������һС���Ƶ��Ϊx����Ƶ�ʷֲ�ֱ��ͼ��6x+��0.037+0.013����5=1���ɴ������������������
������Ƶ�ʷֲ�ֱ��ͼ��������س���60�����ѧ����ռƵ�ʣ�������X�п���ȡֵΪ0��1��2��3����X��B��3��0.625�����ɴ�������X�ķֲ��к�EX��
��� �⣺���ߴ����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3�����е�2С���Ƶ��Ϊ12��
�����һС���Ƶ��Ϊx����Ƶ�ʷֲ�ֱ��ͼ�ã�
6x+��0.037+0.013����5=1�����x=0.125��
��ڶ�С���Ƶ��Ϊ2x=0.25��
������������n=$\frac{12}{0.25}$=48��
������Ƶ�ʷֲ�ֱ��ͼ�������س���60�����ѧ����ռƵ��Ϊ��0.125��3+��0.037+0.013����5=0.625��
��ȫʡ�߶��꼶������ѧ���У������ࣩܶ��ѡ���ˣ���X��ʾ���س���60�����ѧ��������
��X�п���ȡֵΪ0��1��2��3����X��B��3��0.625����
P��X=0��=${C}_{3}^{0}$0.3753=0.052734375��
P��X=1��=${C}_{3}^{1}•0.625•0.37{5}^{2}$=0.263671875��
P��X=2��=${C}_{3}^{2}��0.625��^{2}•0.375$=0.439453125��
P��X=3��=${C}_{3}^{3}��0.625��^{3}$=0.244140625��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | 0.052734375 | 0.263671875 | 0.439453125 | 0.244140625 |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{��}$ | B�� | $\frac{2}{��}$ | C�� | $\frac{1}{{��}^{2}}$ | D�� | $\frac{2}{{��}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | -1 | C�� | -2 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
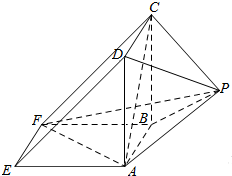 ��ͼ��ʾ���ü���������һ��ֱ������ADE-BCF��һ��������P-ABCD��϶��ɣ�AD��AF��AE=AD=2��
��ͼ��ʾ���ü���������һ��ֱ������ADE-BCF��һ��������P-ABCD��϶��ɣ�AD��AF��AE=AD=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $2\sqrt{2}$ | C�� | 2 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
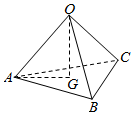
| A�� | $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$ | B�� | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | C�� | $\frac{1}{2}$��$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$�� | D�� | $\frac{1}{3}$��$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{7}{8}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com