Question

18．设三棱锥O-ABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，G是△ABC的重心，则$\overrightarrow{OG}$等于（　　）

• A． $\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$
• B． $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$
• C． $\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$）
• D． $\frac{1}{3}$（$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$）

Answer 1

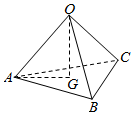
分析 $\overrightarrow{OG}$=$\overrightarrow{OA}+\overrightarrow{AG}$，设AG的延长线与BC相交于点D，由于G是△ABC的重心，可得$\overrightarrow{AG}$=$\frac{2}{3}\overrightarrow{AD}$，$\overrightarrow{AD}$=$\frac{1}{2}（\overrightarrow{AC}+\overrightarrow{AB}）$，$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}$，$\overrightarrow{AB}$=$\overrightarrow{OB}-\overrightarrow{OA}$，化简即可得出．

解答 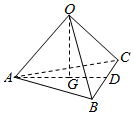解：$\overrightarrow{OG}$=$\overrightarrow{OA}+\overrightarrow{AG}$，
设AG的延长线与BC相交于点D，
∵G是△ABC的重心，
∴$\overrightarrow{AG}$=$\frac{2}{3}\overrightarrow{AD}$，$\overrightarrow{AD}$=$\frac{1}{2}（\overrightarrow{AC}+\overrightarrow{AB}）$，$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}$，$\overrightarrow{AB}$=$\overrightarrow{OB}-\overrightarrow{OA}$，
则$\overrightarrow{OG}$=$\frac{1}{3}\overrightarrow{OA}$+$\frac{1}{3}\overrightarrow{OB}$+$\frac{1}{2}\overrightarrow{OC}$
=$\frac{1}{3}（\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}）$，
故选：D．

点评 本题考查了重心的性质、向量的三角形法则、向量的平行四边形法则，考查了推理能力与计算能力，属于中档题．