
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
分析 易知f(a)=ln(2a+$\sqrt{4{a}^{2}+1}$)-$\frac{2}{{2}^{a}+1}$=1,化简f(-a)=ln(-2a+$\sqrt{4{a}^{2}+1}$)-$\frac{2}{{2}^{-a}+1}$=ln($\frac{1}{\sqrt{4{a}^{2}+1}+2a}$)-$\frac{2•{2}^{a}}{{2}^{a}+1}$,从而求得.
解答 解:由题意知,
f(a)=ln(2a+$\sqrt{4{a}^{2}+1}$)-$\frac{2}{{2}^{a}+1}$=1,
故f(-a)=ln(-2a+$\sqrt{4{a}^{2}+1}$)-$\frac{2}{{2}^{-a}+1}$
=ln($\frac{1}{\sqrt{4{a}^{2}+1}+2a}$)-$\frac{2•{2}^{a}}{{2}^{a}+1}$
=-ln(2a+$\sqrt{4{a}^{2}+1}$)-2+$\frac{2}{{2}^{a}+1}$
=-(ln(2a+$\sqrt{4{a}^{2}+1}$)-$\frac{2}{{2}^{a}+1}$)-2=-3,
故选:D.
点评 本题考查了学生的化简运算能力.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{15}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,点D在边AB上,CD⊥BC,AC=5$\sqrt{3}$,CD=5,BD=2AD.
如图,在△ABC中,点D在边AB上,CD⊥BC,AC=5$\sqrt{3}$,CD=5,BD=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 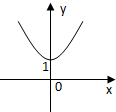 | B. | 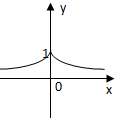 | C. |  | D. | 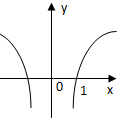 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解荆州中学学生健康状况,从去年高二年级体检表中抽取若干份,将他们的体重数据作为样本.将样本的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解荆州中学学生健康状况,从去年高二年级体检表中抽取若干份,将他们的体重数据作为样本.将样本的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{6}$ | D. | π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com