
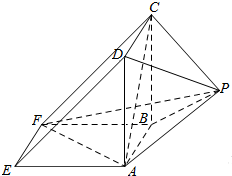
 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.分析 (Ⅰ)证明:AD⊥平面ABFE,即可证明平面PAD⊥平面ABFE;
(Ⅱ)利用体积公式,即可求正四棱锥P-ABCD的高.
解答  (Ⅰ)证明:直三棱柱ADE-BCF中,AB⊥平面ADE,
(Ⅰ)证明:直三棱柱ADE-BCF中,AB⊥平面ADE,
所以:AB⊥AD,又AD⊥AF,
所以:AD⊥平面ABFE,AD?平面PAD,
所以:平面PAD⊥平面ABFE….(6分)
(Ⅱ)P到平面ABCD的距离d=1
所以:${V_{P-ABF}}=\frac{1}{3}{S_{△ABF}}d=\frac{1}{3}×\frac{1}{2}×2×2×1=\frac{2}{3}$
而:${V_{P-ABCD}}=\frac{1}{3}{S_{ABCD}}h=\frac{1}{3}×2×2h=4{V_{P-ABF}}=\frac{8}{3}$,
所以h=2….(12分)
点评 本题考查直线与平面、平面与平面垂直的证明,求三棱锥的体积,解题时要认真审题,注意合理地化立体几何问题为平面几何问题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | 至少有一个成立 | B. | 至多有一个成立 | C. | 都不成立 | D. | 可以同时成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 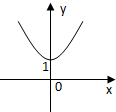 | B. | 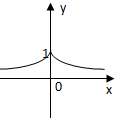 | C. |  | D. | 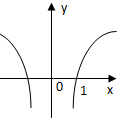 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解荆州中学学生健康状况,从去年高二年级体检表中抽取若干份,将他们的体重数据作为样本.将样本的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解荆州中学学生健康状况,从去年高二年级体检表中抽取若干份,将他们的体重数据作为样本.将样本的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com