
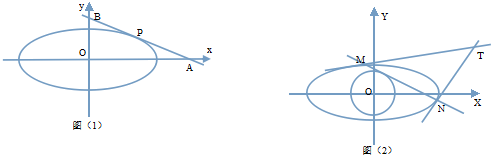
分析 (1)由椭圆的离心率公式和基本量a,b,c的关系,解得a=2,b=c=$\sqrt{2}$,进而得到椭圆方程;
(2)(i)设P(2cosα,$\sqrt{2}$sinα)(0<α<$\frac{π}{2}$),求得切线的方程,分别令x=0,y=0,可得y轴、x轴上的截距,再由三角形的面积公式,结合二倍角公式和正弦函数的最值,可得最小值;
(ii)设M(x1,y1),N(x2,y2),求得M,N处椭圆的切线方程,设T(m,n),代入切线方程,运用两点确定一条直线,可得切点弦方程,再由直线和圆相切的条件:d=r,可得T的轨迹方程,即为椭圆,再由椭圆的定义,即可得证.
解答 解:(1)椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,
一个短轴端点到焦点的距离为2.
可得e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,$\sqrt{{b}^{2}+{c}^{2}}$=2,a2-b2=c2,
解得a=2,b=c=$\sqrt{2}$,
则椭圆C1的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;
(2)(i)设P(2cosα,$\sqrt{2}$sinα)(0<α<$\frac{π}{2}$),
则切线l的方程为$\frac{2cosαx}{4}$+$\frac{\sqrt{2}sinαx}{2}$=1,
即为xcosα+$\sqrt{2}$ysinα-2=0,
由x=0,可得y=$\frac{2}{\sqrt{2}sinα}$;y=0,可得x=$\frac{2}{cosα}$.
即有△OAB面积为S=$\frac{1}{2}$•$\frac{2}{\sqrt{2}sinα}$•$\frac{2}{cosα}$=$\frac{4}{\sqrt{2}sin2α}$≥$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
当2α=$\frac{π}{2}$,即α=$\frac{π}{4}$时,S取得最小值2$\sqrt{2}$;
(ii)证明:设M(x1,y1),N(x2,y2),
可得M,N点处的切线方程为$\frac{{x}_{1}x}{4}$+$\frac{{y}_{1}y}{2}$=1,
$\frac{{x}_{2}x}{4}$+$\frac{{y}_{2}y}{2}$=1,
设T(m,n),可得$\frac{m{x}_{1}}{4}$+$\frac{n{y}_{1}}{2}$=1,$\frac{m{x}_{2}}{4}$+$\frac{n{y}_{2}}{2}$=1,
由两点确定一条直线,可得切点弦MN的方程为$\frac{mx}{4}$+$\frac{ny}{2}$=1,
即为mx+2ny-4=0.
由MN与圆O相切,可得$\frac{|0+0-4|}{\sqrt{{m}^{2}+4{n}^{2}}}$=1,
化简可得$\frac{{m}^{2}}{16}$+$\frac{{n}^{2}}{4}$=1,
即为T的轨迹方程,显然为焦点在x轴上的椭圆.
由$E(-2\sqrt{3},0),F(2\sqrt{3},0)$,即为椭圆的两焦点,
由椭圆的定义可得|TE|+|TF|为定值,且为长轴长2×4=8.
点评 本题考查椭圆的方程的求法,注意运用离心率公式,考查椭圆的切线的方程和应用,同时考查切点弦方程的求法,直线和圆相切的条件:d=r,考查轨迹方程的求法和椭圆的定义的运用,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
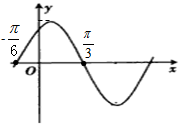 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
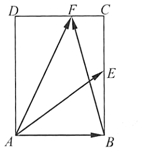 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值是( )| A. | 2-$\sqrt{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,0) | C. | (1,+∞) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com