
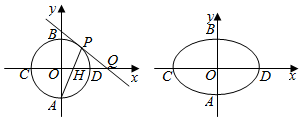
 已知圆C1:x2+y2=r2和椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
已知圆C1:x2+y2=r2和椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).分析 (1)过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)一点P(x0,y0)作椭圆的切线为:$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1,下面给出证明:由$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$=1,可得${b}^{2}{x}_{0}^{2}+{a}^{2}{y}_{0}^{2}-{a}^{2}{b}^{2}$=0.
y0≠0时,y=$\frac{{b}^{2}}{{y}_{0}}(1-\frac{{x}_{0}x}{{a}^{2}})$代入椭圆方程,只要证明△=0即可.y0=0时,直径验证即可得出结论.
(2)设A,B,C,D分别是椭圆C2与坐标轴的四个交点,过椭圆C2上任意一点P(x0,y0)(不与A,B,C,D重合)的切线交x轴于点Q,连接PA交x轴于点H,则QD,QH,QC成等比数列.下面给出证明分析:由(1)可知:过椭圆C2上任意一点P(x0,y0)(不与A,B,C,D重合)的切线方程为:$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1.(x0,y0)≠(0,0),不妨设x0>0,y0>0.令y=0,可得Q$(\frac{{a}^{2}}{{x}_{0}},0)$,可得QD,QC.由点斜式可得直线AP的方程为:$y=\frac{{y}_{0}+b}{{x}_{0}}$x-b,令y=0,可得xH,QH2.只要证明QD•QC=QH2即可得出结论.
解答  解:(1)过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)一点P(x0,y0)作椭圆的切线为:$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1,
解:(1)过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)一点P(x0,y0)作椭圆的切线为:$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1,
下面给出证明:由$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$=1,可得${b}^{2}{x}_{0}^{2}+{a}^{2}{y}_{0}^{2}-{a}^{2}{b}^{2}$=0.
y0≠0时,y=$\frac{{b}^{2}}{{y}_{0}}(1-\frac{{x}_{0}x}{{a}^{2}})$代入椭圆方程可得:$({a}^{2}{y}_{0}^{2}+{b}^{2}{x}_{0}^{2})$x2-2a2b2x0x+${a}^{4}({b}^{2}-{y}_{0}^{2})$=0,
△=$4{a}^{4}{b}^{4}{x}_{0}^{2}$-4${a}^{4}({b}^{2}-{y}_{0}^{2})$$({a}^{2}{y}_{0}^{2}+{b}^{2}{x}_{0}^{2})$=4a4${y}_{0}^{2}$$({a}^{2}{y}_{0}^{2}+{b}^{2}{x}_{0}^{2}-{a}^{2}{b}^{2})$=0.
∴$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1为椭圆的切线.
y0=0时,x0=±a,椭圆的切线为x=±a,也满足上式.
综上可得:过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)一点P(x0,y0)作椭圆的切线为:$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1.
(2)设A,B,C,D分别是椭圆C2与坐标轴的四个交点,过椭圆C2上任意一点P(x0,y0)(不与A,B,C,D重合)的切线交x轴于点Q,连接PA交x轴于点H,则QD,QH,QC成等比数列.
下面给出证明:由(1)可知:
过椭圆C2上任意一点P(x0,y0)(不与A,B,C,D重合)的切线方程为:$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1.(x0,y0)≠(0,0),不妨设x0>0,y0>0.
令y=0,可得Q$(\frac{{a}^{2}}{{x}_{0}},0)$,∴QD=$\frac{{a}^{2}}{{x}_{0}}$-a,QC=$\frac{{a}^{2}}{{x}_{0}}$+a,∴QD•QC=($\frac{{a}^{2}}{{x}_{0}}$-a)(=$\frac{{a}^{2}}{{x}_{0}}$+a)=$\frac{{a}^{4}}{{x}_{0}^{2}}$-a2.
∵$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$=1,可得${x}_{0}^{2}$=$\frac{{a}^{2}}{{b}^{2}}({b}^{2}-{y}_{0}^{2})$.
∴QD•QC=$\frac{{a}^{2}{y}_{0}^{2}}{{b}^{2}-{y}_{0}^{2}}$.
直线AP的方程为:$y=\frac{{y}_{0}+b}{{x}_{0}}$x-b,令y=0,可得xH=$\frac{b{x}_{0}}{{y}_{0}+b}$,
∴QH=$\frac{{a}^{2}}{{x}_{0}}$-$\frac{b{x}_{0}}{{y}_{0}+b}$,∴QH2=$\frac{{a}^{4}}{{x}_{0}^{2}}$+$\frac{{b}^{2}{x}_{0}^{2}}{({y}_{0}+b)^{2}}$-$\frac{2{a}^{2}b}{{y}_{0}+b}$=$\frac{{a}^{2}{y}_{0}^{2}}{{b}^{2}-{y}_{0}^{2}}$.
∴QD•QC=QH2.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、基本不等式的性质、线段的垂直平分线的性质,考查了推理能力与计算能力,属于难题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-1,0) | C. | (0,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
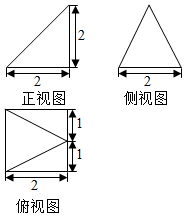 已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为$\frac{8}{3}$,表面积为$6+2\sqrt{5}+2\sqrt{2}$.
已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为$\frac{8}{3}$,表面积为$6+2\sqrt{5}+2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}$-y2=1 | B. | x2-$\frac{y^2}{4}$=1 | C. | $\frac{x^2}{5}$-$\frac{y^2}{4}$=1 | D. | 5x2-$\frac{{5{y^2}}}{4}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com