
分析 (1)利用绝对值的几何意义求出|2x+1|+|2x-3|的最小值,得到a的不等式求解即可.
(2)通过△≥0,得到|2m+1|+|2m-3|≤8,去掉绝对值求解即可.
解答 解:(1)因为f(x)=|2x+1|+|2x-3|≥|(2x+1)-(2x-3)|=4,
所以|1-3a|<4,即$-1<a<\frac{5}{3}$,
所以实数a的取值范围为$({-1,\frac{5}{3}})$.…(5分)
(2)△=32-4(|2m+1|+|2m-3|)≥0,
即|2m+1|+|2m-3|≤8,
所以不等式等价于$\left\{\begin{array}{l}m>\frac{3}{2}\\(2m+1)+(2m-3)≤8\end{array}\right.$或$\left\{\begin{array}{l}{-\frac{1}{2}≤m≤\frac{3}{2}}\\{2m+1-2m+3≤8}\end{array}\right.$或$\left\{\begin{array}{l}m<-\frac{1}{2}\\-(2m+1)-(2m-3)≤8.\end{array}\right.$
所以$\frac{3}{2}<m≤\frac{5}{2}$,或$-\frac{1}{2}≤m≤\frac{3}{2}$,或$-\frac{3}{2}≤m<-\frac{1}{2}$,
所以实数m的取值范围是$\left\{{m|-\frac{3}{2}≤m≤\frac{5}{2}}\right\}$. …(10分)
点评 本题考查函数恒成立,绝对值不等式的几何意义,二次函数的简单性质的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{\sqrt{14}}{2}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{3\sqrt{2}}{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
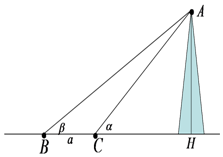 如图,在点B处测得山顶A的仰角为β,在点C处测得山顶A的仰角为α,BC=a,则山高AH为( )
如图,在点B处测得山顶A的仰角为β,在点C处测得山顶A的仰角为α,BC=a,则山高AH为( )| A. | $\frac{asinαsinβ}{{sin({α-β})}}$ | B. | $\frac{asinαcosβ}{{sin({α-β})}}$ | C. | $\frac{acosαsinβ}{{sin({α-β})}}$ | D. | $\frac{acosαcosβ}{{sin({α-β})}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两两相交的三条直线 | |
| B. | 三条直线,它们两两相交,但不交于同一点 | |
| C. | 三个点 | |
| D. | 三条直线,其中的一条与另外两条直线分别相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com