[题目]已知f(x)=x2﹣3.g(x)=mex . 若方程f有三个不同的实根.则m的取值范围是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】已知f（x）=x2﹣3，g（x）=mex ，若方程f（x）=g（x）有三个不同的实根，则m的取值范围是（）
A.
B.
C.
D.（0，2e）

【答案】A
【解析】解：设f（x）与g（x）的共同切线的切点为（x0 ， y0）， ∵f（x）=x2﹣3，g（x）=mex ，
∴f′（x）=2x，g（x）=mex ，
∴f′（x0）=g′（x0），f（x0）=g（x0），
∴2x0= ，x02﹣3= ，
∴x0=x02﹣3，
解得x0=3，或x0=﹣1（舍去）
当x0=3，
∴6=me3 ，即m= ，
∵方程f（x）=g（x）有三个不同的实根，由图象可知，
∴0＜m＜，
故选：A．

设f（x）与g（x）的共同切线的切点为（x0 ， y0），根据导数求出切点，即可求出m的值，结合图象可知m的取值范围．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P－ABCD中，PC⊥底面ABCD，AD∥BC，AD＝2BC＝2，PC＝2，△ABC是以AC为斜边的等腰直角三角形，E是PD的中点．

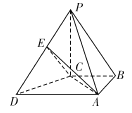
(1)求证：平面EAC⊥平面PCD；

(2)求直线PA与平面EAC所成角的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列和,,,(且), , .

(I)求;

(Ⅱ)猜想数列的通项公式,并证明;

(Ⅲ)设函数,若对任意恒成立,求的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在直角坐标系xOy中，点P（0，），以原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为．直线l的参数方程为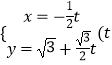为参数）．
（Ⅰ）写出曲线C的直角坐标方程和直线l的普通方程；
（Ⅱ）设直线l与曲线C的两个交点分别为A，B，求 + 的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）是定义在（﹣∞，0）上的可导函数，其导函数为f′（x），且有xf′（x）＞x2+3f（x），则不等式8f（x+2014）+（x+2014）3f（﹣2）＞0的解集为（）
A.（﹣∞，﹣2016）
B.（﹣2018，﹣2016）
C.（﹣2018，0）
D.（﹣∞，﹣2018）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知双曲线 ﹣ =1（a＞0，b＞0）的实轴端点分别为A1 ， A2 ，记双曲线的其中的一个焦点为F，一个虚轴端点为B，若在线段BF上（不含端点）有且仅有两个不同的点Pi（i=1，2），使得∠A1PiA2= ，则双曲线的离心率e的取值范围是（）
A.（，）
B.（，）
C.（1，）
D.（，+∞）