
ЁОЬтФПЁПЮЊЕїВщФГЩчЧјОгУёЕФвЕгрЩњЛюзДПіЃЌбаОПетвЛЩчЧјОгУёдк20ЃК00Љ22ЃК00ЪБМфЖЮЕФанЯаЗНЪНгыадБ№ЕФЙиЯЕЃЌЫцЛњЕїВщСЫИУЩчЧј80ШЫЃЌЕУЕНЯТУцЕФЪ§ОнБэЃК
анЯаЗНЪН | ПДЕчЪг | ПДЪщ | КЯМЦ |
Фа | 10 | 50 | 60 |
ХЎ | 10 | 10 | 20 |
КЯМЦ | 20 | 60 | 80 |
ЃЈ1ЃЉИљОнвдЩЯЪ§ОнЃЌФмЗёга99%ЕФАбЮеШЯЮЊЁАдк20ЃК00Љ22ЃК00ЪБМфЖЮОгУёЕФанЯаЗНЪНгыадБ№гаЙиЯЕЁБЃП
ЃЈ2ЃЉНЋДЫбљБОЕФЦЕТЪЙРМЦЮЊзмЬхЕФИХТЪЃЌЫцЛњЕїВщ3УћдкИУЩчЧјЕФФаадЃЌЩшЕїВщЕФ3ШЫдкетвЛЪБМфЖЮвдПДЪщЮЊанЯаЗНЪНЕФШЫЪ§ЮЊЫцЛњБфСПXЃЎЧѓXЕФЪ§бЇЦкЭћКЭЗНВюЃЎ
PЃЈX2ЁнkЃЉ | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
ИНЃКX2= ![]() ЃЎ
ЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКИљОнбљБОЬсЙЉЕФ2ЁС2СаСЊБэЕУЃКX2= ![]() Ёж8.889ЃО6.635ЃЛ
Ёж8.889ЃО6.635ЃЛ
Ыљвдга99%ЕФАбЮеШЯЮЊЁАдк20ЃК00Љ22ЃК00ЪБМфЖЮОгУёЕФанЯаЗНЪНгыадБ№гаЙиЃЎ
ЃЈ2ЃЉНтЃКгЩЬтвтЕУЃКXЁЋBЃЈ3ЃЌ ![]() ЃЉЃЌЫљвдEЃЈXЃЉ=3ЁС
ЃЉЃЌЫљвдEЃЈXЃЉ=3ЁС ![]() =
= ![]() ЃЌDЃЈXЃЉ=3ЁС
ЃЌDЃЈXЃЉ=3ЁС ![]() ЁС
ЁС ![]() =
= ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉИљОнбљБОЬсЙЉЕФ2ЁС2СаСЊБэЃЌЕУЕБH0ГЩСЂЪБЃЌK2Ён6.635ЕФИХТЪдМЮЊ0.01ЃЌгЩДЫФмЭЦЕМГіга99%ЕФАбЮеШЯЮЊЁАдк20ЃК00Љ22ЃК00ЪБМфЖЮЕФанЯаЗНЪНгыадБ№гаЙиЯЕЃЎЃЈ2ЃЉгЩЬтвтЕУЃКXЁЋBЃЈ3ЃЌ ![]() ЃЉЃЌгЩДЫФмЧѓГіXЕФЪ§бЇЦкЭћКЭЗНВюЃЎ
ЃЉЃЌгЩДЫФмЧѓГіXЕФЪ§бЇЦкЭћКЭЗНВюЃЎ


 ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ
ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ бєЙтПМГЁЕЅдЊВтЪдОэЯЕСаД№АИ
бєЙтПМГЁЕЅдЊВтЪдОэЯЕСаД№АИ УћаЃСЊУЫГхДЬОэЯЕСаД№АИ
УћаЃСЊУЫГхДЬОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-5ЃКВЛЕШЪНбЁНВ
вбжЊКЏЪ§![]()
ЃЈ1ЃЉЧѓВЛЕШЪН![]() ЕФНтМЏ
ЕФНтМЏ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
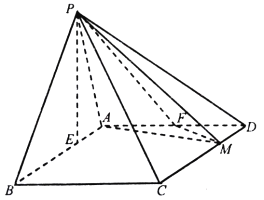
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ
ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ![]() ЃЌзѓЁЂгвЖЅЕуЗжБ№ЮЊ
ЃЌзѓЁЂгвЖЅЕуЗжБ№ЮЊ![]() ЮЊжБОЖЕФдВOЙ§ЭждВEЕФЩЯЖЅЕуDЃЌжБЯпDBгыдВOЯрНЛЕУЕНЕФЯвГЄЮЊ
ЮЊжБОЖЕФдВOЙ§ЭждВEЕФЩЯЖЅЕуDЃЌжБЯпDBгыдВOЯрНЛЕУЕНЕФЯвГЄЮЊ![]() ЃЎЩшЕу
ЃЎЩшЕу![]() ЃЌСЌНгPAНЛЭждВгкЕуCЃЎ
ЃЌСЌНгPAНЛЭждВгкЕуCЃЎ
(I)ЧѓЭждВEЕФЗНГЬЃЛ
(II)ШєШ§НЧаЮABCЕФУцЛ§ВЛДѓгкЫФБпаЮOBPCЕФУцЛ§ЃЌЧѓtЕФзюаЁжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
ЃЈ1ЃЉЩш![]() ЃЌЪдЬжТл
ЃЌЪдЬжТл![]() ЕЅЕїадЃЛ
ЕЅЕїадЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌШЮвт
ЪБЃЌШЮвт![]() ЃЌДцдк
ЃЌДцдк![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЮЊЦНааЫФБпаЮЃЌ
ЮЊЦНааЫФБпаЮЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕудкЕзУц
ЕудкЕзУц![]() ФкЕФЩфгА
ФкЕФЩфгА![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЕБ![]() ЪБЃЌжЄУїЃКЦНУц
ЪБЃЌжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЕБЦНУц![]() гыЦНУц
гыЦНУц![]() ЫљГЩЕФЖўУцНЧЕФе§ЯвжЕЮЊ
ЫљГЩЕФЖўУцНЧЕФе§ЯвжЕЮЊ![]() ЪБЃЌЧѓЫФРтзЖ
ЪБЃЌЧѓЫФРтзЖ![]() ЕФЬхЛ§ЃЎ
ЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ЕФЧАnЯюКЭЮЊSn ЃЌ ЧвТњзуSn=2anЉ2ЃЎ
ЃЈЂёЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈЂђЃЉЩшКЏЪ§fЃЈxЃЉ=ЃЈ ![]() ЃЉx ЃЌ Ъ§Са{bn}ТњзуЬѕМўb1=2ЃЌfЃЈbn+1ЃЉ=
ЃЉx ЃЌ Ъ§Са{bn}ТњзуЬѕМўb1=2ЃЌfЃЈbn+1ЃЉ= ![]() ЃЌЃЈnЁЪN*ЃЉЃЌШєcn=
ЃЌЃЈnЁЪN*ЃЉЃЌШєcn= ![]() ЃЌЧѓЪ§Са{cn}ЕФЧАnЯюКЭTn ЃЎ
ЃЌЧѓЪ§Са{cn}ЕФЧАnЯюКЭTn ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєВЛЕШЪНx2ЉaxЉbЃМ0ЕФНтМЏЪЧ{x|2ЃМxЃМ3}ЃЌЧѓВЛЕШЪНbx2ЉaxЉ1ЃО0ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPЉABCDжаЃЌЕзУцABCDЪЧе§ЗНаЮЃЌВрРтPDЁЭЕзУцABCDЃЌPD=DC=2ЃЌEЪЧPCЕФжаЕуЃЌзїEFЁЭPBНЛPBгкЕуFЃЎ 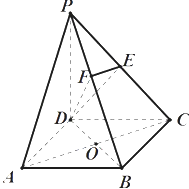
ЃЈ1ЃЉжЄУї PAЁЮЦНУцEDBЃЛ
ЃЈ2ЃЉжЄУїPBЁЭЦНУцEFDЃЛ
ЃЈ3ЃЉЧѓVBЉEFD ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊУќЬтpЃКЗНГЬ ![]() =1БэЪОНЙЕудкyжсЩЯЕФЭждВЃЛУќЬтqЃКЫЋЧњЯп
=1БэЪОНЙЕудкyжсЩЯЕФЭждВЃЛУќЬтqЃКЫЋЧњЯп ![]() Љ
Љ ![]() =1ЕФРыаФТЪeЁЪЃЈ1ЃЌ2ЃЉЃЎШєУќЬтpЁЂqгаЧвжЛгавЛИіЮЊецЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
=1ЕФРыаФТЪeЁЪЃЈ1ЃЌ2ЃЉЃЎШєУќЬтpЁЂqгаЧвжЛгавЛИіЮЊецЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com