
分析 (1)根据向量的坐标运算和向量的夹角公式即可求出,
(2)根据向量的垂直的条件,即$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,代值计算即可.
解答 解:(1)当m=-3时,$\overrightarrow{OC}$=(-3,-4),
∵量$\overrightarrow{OA}$=(-2,4),$\overrightarrow{OB}$=(3,-1),
∴$\overrightarrow{AB}$=(5,-5),$\overrightarrow{BC}$=(-6,-3),
∴$\overrightarrow{AB}•\overrightarrow{BC}$=5×(-6)+(-5)×(-3)=-15,
|$\overrightarrow{AB}$|=5$\sqrt{2}$,$\overrightarrow{BC}$=3$\sqrt{5}$,
∴cos<$\overrightarrow{AB}$,$\overrightarrow{BC}$>=$\frac{\overrightarrow{AB}•\overrightarrow{BC}}{|\overrightarrow{AB}|•|\overrightarrow{BC}|}$=$\frac{-15}{5\sqrt{2}•3\sqrt{5}}$=-$\frac{\sqrt{10}}{10}$,
(2)由(1)知$\overrightarrow{AB}$=(5,-5),$\overrightarrow{AC}$=(m+2,-8),
∵∠A为直角,
∴$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=0,
即5(m+2)+40=0,
解得m=-10
点评 本题考查了向量的夹角公式和向量的垂直的条件,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -b+4 | B. | -b+2 | C. | b-2 | D. | b+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
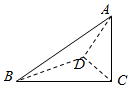 已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BD⊥AD,且AD=2$\sqrt{5}$,BD=2,CD=$\sqrt{3}$,则球O的体积为( )
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BD⊥AD,且AD=2$\sqrt{5}$,BD=2,CD=$\sqrt{3}$,则球O的体积为( )| A. | 8$\sqrt{6}$π | B. | $\frac{27\sqrt{3}π}{2}$ | C. | $\frac{7\sqrt{7}π}{6}$ | D. | 10$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
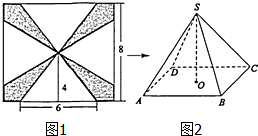 一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为$\frac{3\sqrt{2}}{5}$.
一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为$\frac{3\sqrt{2}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 运行如图的程序,如果输入的m,n的值分别是24和15,记录输出的i和m的值.在平面直角坐标系xOy中,已知点A(i-4,m),圆C的圆心在直线l:y=2x-4上.
运行如图的程序,如果输入的m,n的值分别是24和15,记录输出的i和m的值.在平面直角坐标系xOy中,已知点A(i-4,m),圆C的圆心在直线l:y=2x-4上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{10}$ | B. | 3 | C. | 4 | D. | $\frac{21}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com