
 一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为$\frac{3\sqrt{2}}{5}$.
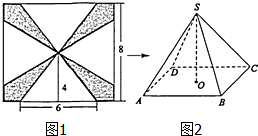
一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为$\frac{3\sqrt{2}}{5}$. 分析 连接OC,则∠SCO为侧棱SC与底面ABCD所成角,根据图1可知棱锥底面边长为6,斜高为4,从而棱锥的侧棱长为5.于是cos∠SCO=$\frac{OC}{SC}$.
解答 解: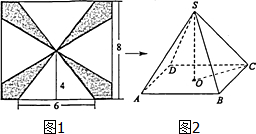 由图1可知四棱锥的底面边长为6,斜高为4.
由图1可知四棱锥的底面边长为6,斜高为4.
∴棱锥的侧棱长为5.
连接OC,
∵SO⊥平面ABCD,
∴∠SCO为侧棱SC与底面ABCD所成的角.
∵AB=BC=6,
∴OC=$\frac{1}{2}$AC=3$\sqrt{2}$.
∴cos∠SCO=$\frac{OC}{SC}$=$\frac{3\sqrt{2}}{5}$.
故答案为:$\frac{3\sqrt{2}}{5}$.
点评 本题考查了棱锥的结构特征,线面角的计算,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{π}$ | D. | $\frac{1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14π | B. | 12π | C. | 10π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$],k∈Z | B. | [2kπ+$\frac{π}{2}$,2kπ+$\frac{3π}{4}$],k∈Z | ||
| C. | [kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$],k∈Z | D. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$],k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com