
分析 运用二元均值不等式可得$\sqrt{ab}$≥2,再由二项式定理,化简整理可得(a+b)n-(an+bn)
=$\frac{1}{2}[{({a^{n-1}}b+a{b^{n-1}})C_n^1+({a^{n-2}}{b^2}+{a^2}{b^{n-2}})C_n^2+…+(a{b^{n-1}}+{a^{n-1}}b)C_n^{n-1}}]$,再由均值不等式即可得证.
解答 证明:由a,b均大于0,且$\frac{1}{a}$+$\frac{1}{b}$=1,
可得$1=\frac{1}{a}+\frac{1}{b}≥\frac{2}{{\sqrt{ab}}}$知$\sqrt{ab}≥2$,
由二项式定理,得${(a+b)^n}-({a^n}+{b^n})=C_n^1{a^{n-1}}b+C_n^2{a^{n-2}}{b^2}+…+C_n^{n-2}{a^2}{b^{n-2}}+C_n^{n-1}a{b^{n-1}}$
=$\frac{1}{2}[{({a^{n-1}}b+a{b^{n-1}})C_n^1+({a^{n-2}}{b^2}+{a^2}{b^{n-2}})C_n^2+…+(a{b^{n-1}}+{a^{n-1}}b)C_n^{n-1}}]$$≥\sqrt{{{(ab)}^n}}({C_n^1+C_n^2+…+C_n^{n-1}})≥{2^n}({2^n}-2)={2^{2n}}-{2^{n+1}}$.
则原不等式成立.
点评 本题考查不等式的证明,注意运用二元均值不等式和二项式定理,以及二项式系数的性质,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
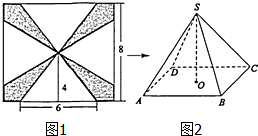 一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为$\frac{3\sqrt{2}}{5}$.
一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为$\frac{3\sqrt{2}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{10}$ | B. | 3 | C. | 4 | D. | $\frac{21}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | 8 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com