
分析 (1)利用诱导公式化简表达式,代入已知条件求解即可.
(2)利用同角三角函数基本关系式化简求解即可.
解答 解:由$tanα=-\frac{3}{2}$,α为第二象限角,解得$cosα=-\frac{2}{13}\sqrt{13}$…(2分)
(1)原式=$\frac{(-cosα)sinα(-tanα)}{(-tanα)sinα}=-cosα$,
故原式=-cosα=$\sqrt{\frac{1}{{1+{{tan}^2}α}}}=\frac{2}{13}\sqrt{13}$…(7分)
(2)$\frac{1}{cosα\sqrt{1+ta{n}^{2}α}}$+$\sqrt{\frac{1+sinα}{1-sinα}}$-$\sqrt{\frac{1-sinα}{1+sinα}}$
=$\frac{1}{cosα\sqrt{\frac{si{n}^{2}α+co{s}^{2}α}{co{s}^{2}α}}}$+$\sqrt{\frac{(1+sinα)^{2}}{1-si{n}^{2}α}}$-$\sqrt{\frac{(1-sinα)^{2}}{1-si{n}^{2}α}}$
=$-1+\frac{1+sinα}{-cosα}+\frac{1-sinα}{cosα}=-1-2tanα=2$…(12分)
点评 本题考查诱导公式以及同角三角函数基本关系式的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
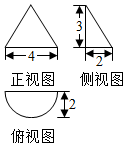
| A. | 2π | B. | 4π | C. | 6+(2+$\sqrt{13}$)π | D. | (4+2$\sqrt{13}$)π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
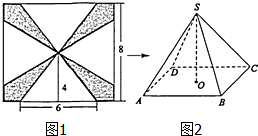 一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为$\frac{3\sqrt{2}}{5}$.
一块边长为8cm的正方形铁板按如图1所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为$\frac{3\sqrt{2}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 感染 | 未感染 | 总计 | |
| 没服用 | 20 | 30 | 50 |
| 服用 | X | y | 50 |
| 总计 | M | N | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{10}$ | B. | 3 | C. | 4 | D. | $\frac{21}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com