
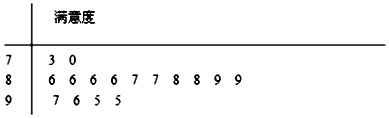
���� ��1�����ִ�����������8.6������С�������У�λ���м����λ����87��88���ɴ��������������λ��
��2���ɾ�Ҷͼ��֪�������Ϊ�������⡱������4�ˣ���Ai��ʾ��ȡ3������i�����ǡ������⡱��������1���ǡ������⡱��Ϊ�¼�A��p��A��=p��A0��+p��A1����
��3����16�˵���������������ѡȡ1�ˣ��鵽�������⡱���˵ĸ���Ϊ$\frac{4}{16}=\frac{1}{4}$�����������֪���Ӹù˿�Ⱥ������ѡ1�ˣ��鵽�������⡱���˵ĸ���p=$\frac{1}{4}$��
�����֪�Ρ�B��3��$\frac{1}{4}$����������εķֲ��м���ѧ������
��� �⣺��1�����ִ�����������8.6������С�������У�λ���м����λ����87��88���ɴ��ܵó���������λ����������8.6����λ����8.75��2���֣�
��2���ɾ�Ҷͼ��֪�������Ϊ�������⡱������4�ˣ�
��Ai��ʾ��ȡ3������i�����ǡ������⡱��������1���ǡ������⡱��Ϊ�¼�A��
p��A��=p��A0��+p��A1��=$\frac{{C}_{12}^{3}}{{C}_{16}^{3}}+\frac{{{C}_{4}^{1}C}_{12}^{2}}{{C}_{16}^{3}}=\frac{121}{140}$
��3����16�˵���������������ѡȡ1�ˣ��鵽�������⡱���˵ĸ���Ϊ$\frac{4}{16}=\frac{1}{4}$��
���������֪���Ӹù˿�Ⱥ������ѡ1�ˣ��鵽�������⡱���˵ĸ���p=$\frac{1}{4}$��
�εĿ���ȡֵΪ0��1��2��3��
p����=0��=��$\frac{3}{4}$��3=$\frac{27}{64}$�� p����=1��=${C}_{3}^{1}��\frac{1}{4}����\frac{3}{4}��^{2}=\frac{27}{64}$��
p����=2��=${C}_{3}^{2}��\frac{1}{4}��^{2}��\frac{3}{4}=\frac{9}{64}$��p����=3��=��$\frac{1}{4}$��3=$\frac{1}{64}$
���Ԧεķֲ���Ϊ
| �� | 0 | 1 | 2 | 3 |
| p | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
���� ���⿼���˶���һ�����ݣ�ͨ��Ҫ������������ݵ���������λ����ƽ��������Ŀ�ֱ��ʾһ�����ݵ�������������������Գ�����ѡ���������⣬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{4}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com