
分析 利用分段函数的单调性求得函数f(t)取得最小值为$\frac{7}{2}$,不等式等价于等价于|2x-1|+|x+2|≤$\frac{7}{2}$,去掉绝对值,转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答 解:由于f(t)=$\left\{\begin{array}{l}{-3t+2,t<-\frac{1}{2}}\\{t+4,-\frac{1}{2}≤t≤3}\\{3t-2,t>3}\end{array}\right.$,故当t=-$\frac{1}{2}$时,函数f(t)取得最小值为$\frac{7}{2}$.
∴不等式|t-3|+|2t+1|≥|2x-1|+|x+2|恒成立,等价于|2x-1|+|x+2|≤$\frac{7}{2}$,
∴$\left\{\begin{array}{l}{x<-2}\\{1-2x-x-2≤\frac{7}{2}}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{-2≤x≤\frac{1}{2}}\\{-(2x-1)+x+2≤\frac{7}{2}}\end{array}\right.$ ②,或 $\left\{\begin{array}{l}{x>\frac{1}{2}}\\{2x-1+x+2≤\frac{7}{2}}\end{array}\right.$③.
解①x∈∅求得,解②求得-$\frac{1}{2}$≤x≤$\frac{1}{2}$,解③求得$\frac{1}{2}$<x≤$\frac{5}{6}$,
综合可得,不等式的解集为{x|-$\frac{1}{2}$≤x≤$\frac{5}{6}$}.
点评 本题主要考查分段函数的应用,函数的恒成立问题,求函数的最值,绝对值不等式的解法,属于中档题.


科目:高中数学 来源: 题型:选择题
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 |
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(万件) | 11 | 10 | 8 | 6 | 5 |
| A. | 14.2元 | B. | 10.8元 | C. | 14.8元 | D. | 10.2元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
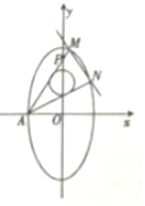 已知在平面直角坐标系xOy中,椭圆$C:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,A是椭圆的左顶点,M,N是椭圆上的两个动点,直线AM交y轴于点P.
已知在平面直角坐标系xOy中,椭圆$C:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,A是椭圆的左顶点,M,N是椭圆上的两个动点,直线AM交y轴于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
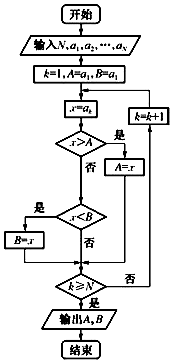 如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )| A. | A+B为a1,a2,…,aN的和 | |
| B. | A和B分别是a1,a2,…,aN中最大的数和最小的数 | |
| C. | $\frac{A+B}{2}$为a1,a2,…,aN的算术平均数 | |
| D. | A和B分别是a1,a2,…,aN中最小的数和最大的数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
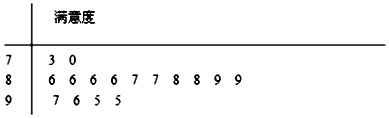
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com