
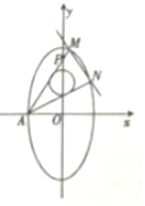
 已知在平面直角坐标系xOy中,椭圆$C:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,A是椭圆的左顶点,M,N是椭圆上的两个动点,直线AM交y轴于点P.
已知在平面直角坐标系xOy中,椭圆$C:\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,A是椭圆的左顶点,M,N是椭圆上的两个动点,直线AM交y轴于点P.分析 (1)因为椭圆的离心率为$\frac{\sqrt{3}}{2}$,得a=2b,椭圆C的方程可设为:y2+4x2=4b2.
设直线AM的方程为:y=k(x+b),代入椭圆方程得(k2+4)x2+2k2bx+(k2-4)b2=0.
$\overrightarrow{AP}=\frac{7}{8}\overrightarrow{AM}$,$0-{x}_{A}=\frac{7}{8}({x}_{M}-{x}_{A})$,b=$\frac{7}{8}[-\frac{({k}^{2}-4)b}{{k}^{2}+4}+b)$,解得k
(2)由(1)知a=2b,又a-b=1,∴a=2,b=1
椭圆C的方程可为:y2+4x2=4.
设切线方程为y=t(x+1),由圆心到其距离为r得(1-r2)t2-2t+1-r2=0.
设AM\AN的斜率分别为t1,t2,则t1t2=1
求出M、N坐标,得直线MN的斜率为kMN=-$\frac{3{t}_{1}}{1+{{t}_{1}}^{2}}$,
直线MN的方程:y-$\frac{8{t}_{1}}{{{t}_{1}}^{2}+4}$=-$\frac{3{t}_{1}}{1+{{t}_{1}}^{2}}$(x-$\frac{4-{{t}_{1}}^{2}}{{{t}_{1}}^{2}+4}$),令y=0,$x=\frac{8{t}_{1}}{{{t}_{1}}^{2}+4}×\frac{1+{{t}_{1}}^{2}}{3{t}_{1}}+\frac{4-{{t}_{1}}^{2}}{{{t}_{1}}^{2}+4}=\frac{5}{3}$.直线MN过定点.
解答 解:(1)因为椭圆的离心率为$\frac{\sqrt{3}}{2}$,∴$\frac{c}{a}=\frac{\sqrt{3}}{2}$又,∵a2=b2+c2,所以a=2b.
椭圆C的方程可设为:y2+4x2=4b2.
设直线AM的方程为:y=k(x+b),代入椭圆方程得(k2+4)x2+2k2bx+(k2-4)b2=0.
∴${x}_{A}{x}_{M}=\frac{({k}^{2}-4){b}^{2}}{{k}^{2}+4}$,⇒xM=$\frac{({k}^{2}-4)b}{{k}^{2}+4}$.
∵$\overrightarrow{AP}=\frac{7}{8}\overrightarrow{AM}$,∴$0-{x}_{A}=\frac{7}{8}({x}_{M}-{x}_{A})$,b=$\frac{7}{8}[-\frac{({k}^{2}-4)b}{{k}^{2}+4}+b)$,解得k2=3.
即直线AM的斜率为$±\sqrt{3}$.
(2)直线MN过定点($\frac{5}{3}$,0)理由如下:
由(1)知a=2b,又a-b=1,∴a=2,b=1
∴椭圆C的方程可为:y2+4x2=4.
设切线方程为y=t(x+1),由圆心到其距离为r,得(1-r2)t2-2t+1-r2=0.
设AM\AN的斜率分别为t1,t2,则t1t2=1
由$\left\{\begin{array}{l}{y=t(x+1)}\\{{y}^{2}+4{x}^{2}=4}\end{array}\right.$可得M($\frac{4-{{t}_{1}}^{2}}{{{t}_{1}}^{2}+4}$,$\frac{8{t}_{1}}{{{t}_{1}}^{2}+4}$)
用$\frac{1}{{t}_{1}}$换t1,得N($\frac{4{{t}_{1}}^{2}-1}{1+4{{t}_{1}}^{2}}$,$\frac{8{t}_{1}}{1+4{{t}_{1}}^{2}}$),∴直线MN的斜率为kMN=-$\frac{3{t}_{1}}{1+{{t}_{1}}^{2}}$,
直线MN的方程:y-$\frac{8{t}_{1}}{{{t}_{1}}^{2}+4}$=-$\frac{3{t}_{1}}{1+{{t}_{1}}^{2}}$(x-$\frac{4-{{t}_{1}}^{2}}{{{t}_{1}}^{2}+4}$)
令y=0,$x=\frac{8{t}_{1}}{{{t}_{1}}^{2}+4}×\frac{1+{{t}_{1}}^{2}}{3{t}_{1}}+\frac{4-{{t}_{1}}^{2}}{{{t}_{1}}^{2}+4}=\frac{5}{3}$.
直线MN过定点($\frac{5}{3}$,0).
点评 本题考查了椭圆的方程,直线与圆、椭圆的位置关系,及直线过定点问题,属于压轴题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
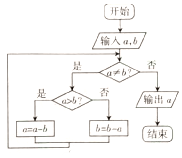 秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( )
秦九韶是我国南宋时期的数学家,他所著的《九章算术》是我国古代数学名著,体现了我国古代数学的辉煌成就.其中的“更相减损术”蕴含了丰富的思想,根据“更相减损术”的思想设计了如图所示的程序框图,若输入的a=15,输出的a=3,则输入的b可能的值为( )| A. | 30 | B. | 18 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
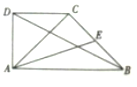 如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.
如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com