
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)根据a[ln(2t-1)-lnt2]≥2[(2t-1)-t2]恒成立,得到t=1时,不等式显然恒成立,当t>1时,问题转化为$a≤\frac{{2[{({2t-1})-{t^2}}]}}{{ln({2t-1})-ln{t^2}}}$,在t>1上恒成立,令$u=\frac{{2[{({2t-1})-{t^2}}]}}{{ln({2t-1})-ln{t^2}}}$,根据函数的单调性求出a的范围即可.
解答 解:(1)$f'(x)=2x+2+\frac{a}{x}=\frac{{2{x^2}+2x+a}}{x}({x>0})$,
令g(x)=2x2+2x+a,判别式为:△=4-8a,
①:当△=4-8a≤0,得$a≥\frac{1}{2}$,
此时g(x)≥0,从而f'(x)≥0,
所以f(x)在(0,+∞)上单调递增.
②:当△=4-8a>0,即$a<\frac{1}{2}$,
令g(x)=2x2+2x+a=0,得方程的根${x_1}=-1-\sqrt{1-2a}$(舍去),${x_2}=-1+\sqrt{1-2a}$,
若a<0,此时x2>0,g(x)>0,得$x>{x_2}=-1+\sqrt{1-2a}$,
由g(x)<0,得$x<{x_2}=-1+\sqrt{1-2a}$,
∴f(x)在$({-1+\sqrt{1-2a},+∞})$上单调递增,在$({0,-1+\sqrt{1-2a}})$单调递减,
若$0≤a<\frac{1}{2}$,此时g(x)=2x2+2x+a的对称轴为$x=-\frac{1}{2}$,g(0)=a>0,
∴g(x)>g(0)=a>0,从而f(x)在(0,+∞)上单调递增.
综上:当a≥0,f(x)在(0,+∞)上单调递增;
当a<0,f(x)在$({-1+\sqrt{1-2a},+∞})$上单调递增,$({0,-1+\sqrt{1-2a}})$单调递减.
(2)由题意有(2t-1)2+2(2t-1)+aln(2t-1)≥2t2+4t+2alnt-3恒成立,
即a[ln(2t-1)-2lnt]≥-2t2+4t-2,
即a[ln(2t-1)-lnt2]≥2[(2t-1)-t2]恒成立,
当t=1时,不等式显然恒成立,
当t>1时,t2-(2t-1)=(t-1)2>0,
所以t2>2t-1,则lnt2>ln(2t-1),
于是$a≤\frac{{2[{({2t-1})-{t^2}}]}}{{ln({2t-1})-ln{t^2}}}$,在t>1上恒成立,
令$u=\frac{{2[{({2t-1})-{t^2}}]}}{{ln({2t-1})-ln{t^2}}}$,
设A(t2,lnt2),B(2t-1,ln(2t-1)),
则${k_{AB}}=\frac{{({2t-1})-{t^2}}}{{ln({2t-1})-ln{t^2}}}$,且A,B两点在y=lnx的图象上,
又t2>1,2t-1>1,
故0<kAB<y'|x=1=1,
所以$u=2\frac{1}{{{k_{AB}}}}>2$,
故a≤2为所求.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥α,n⊥β,m∥n,则α∥β | ||
| C. | 若m⊥α,n∥β,m⊥n,则α∥β | D. | 若m⊥α,n⊥β,m∥n,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
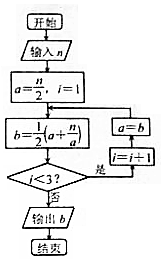 一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n=12,则输出的结果b=( )
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的n=12,则输出的结果b=( )| A. | 4 | B. | $\frac{7}{2}$ | C. | $\frac{97}{28}$ | D. | $\frac{64}{14}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{3}})$ | B. | $({1,\sqrt{6}})$ | C. | $({1,2\sqrt{3}})$ | D. | $({\sqrt{3},3\sqrt{3}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com